scribe, transformation.
 Hi! I'm jessica. and I volunteered to do this scribe today since noone wanted too =/ Boo to you guys I guess. To start off with the morning class. Mr. K gave us questions on the board to do and here they are:
Hi! I'm jessica. and I volunteered to do this scribe today since noone wanted too =/ Boo to you guys I guess. To start off with the morning class. Mr. K gave us questions on the board to do and here they are:
Given the graph of y=F(x) sketch:
A. y=-2F(x) B. y=F(-2x) C. y=-F(x/2) D. -1/2F(-x)
For y=-2F(x), you multiply the y-coordinates by -2 (which will also produce a reflection over the x-axis). For y=F(-2x), you multiply the x-coordinates by 1/2 (which will also produce a reflection over the y-axis). For y=-F(x/2), you multiply the x-coordinates by 2 (which will also produce a reflection over the x-axis). And finally for -1/2F(-x), you multiply the y-coordinates by -2 (which will also produce a reflection over the x-axis) and you multiply the x-coordinates by -1 (which will produce a reflection over the y-axis).
If F(x)=x2-1, write the equation of:
A. y=F(x+2)
How you would do this is by taking the F(x+2) and substituting it into F(x) in the original function that was given to you.
Which would equal y=(x+2)2-1
B. y=F(1/2x)+1
For this one, you square everything in the brackets. Which would give you 1/4x2+1. Since it's a positive 1, it would cancel the negative 1 in the original function. Which will equal to y=1/4x2
C. y=-F(x-1)+2
What you would do is substitute the (x-1) into F(x). Which will give you (x-1)2+2. Don't forget the negative infront of the F, which will be distributed to (x-1)2 and to the negative 1 in the original function ( which will become a positive 1). Then it will all equal to y=-(x-1)2+3
D. y=2F(1-x)+3
How you would do this type of question is by substituting the (1-x) into F(x) in the original function. Then you would multiply 2 to the negative 1 in the original function (which will give you a negative 2). Then 3 subtract negative 2 is positive 1.
You would then get y=2(1-x)2+1
For some people, it may be confusing to get F(1-x). What you would do is factor the negative out. Which you would get is F[-(-1+x)] agreed? Okay, then just rearrange the x to be first. Which will look like.. F[-(x-1)].
Then Mr. K gave us F(2-x) to make an equation from F(x)=(x-1)3
You would do the samething as the above question. Factor out the negative, then rearrange the x.. Which you would get F[-(x-2)]
The black cubic is the original graph. Then the graph was reflected over the y-axis (which is the dotted red line). Then you would shift the red line 2 units to the right.
In the afternoon class, Mr. K gave us notes to write in our math dictionaries.
Transformation:
Translations F(x-a)+b
The role of parameter a:
a>0 the graph shifts right a units.
- the x-coordinates are increased a units.
a<0 the graph shifts left a units.
- the x-coordinates are decreased a units.
WARNING: watch the sign of a
The role of parameter b:
b>0 the graph shifts up b units.
- the y-coordinates are increased b units.
b<0 the graph shifts down b units.
- the y-coordinates are decreased b units.
EXAMPLES: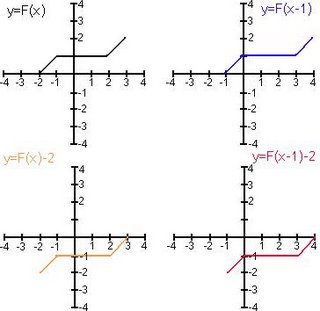
Stretches and Compressions: aF(bx)
The role of parameter a:
a>1 the graph of F(x) is stretched vertically.
0<|a|<1 the graph of F(x) is compressed vertically.
- the y-coordinates of F are multiplied by a.
The role of parameter b:
b>1 the graph of F(x) is compressed horizontally.
(Everything "speeds up")
0<|b|<1 the graph of F(x) is stretched horizontally. (Everything "slows down")
- the x-coordinates are multiplied by 1/b.
EXAMPLES: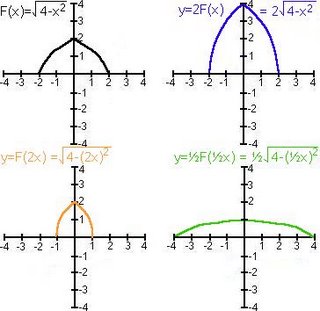
Reflections:
Given any function F(x):
-F(x) produces a reflection in the x-axis.
- y-coordinates are multiplied by (-1)
F(-x) produces a reflection in the y-axis.
- x-coordinates are multiplied by (-1)
Inverses: the inverse of any function.
F(x) is F-1(x) (read as: "EFF INVERSE")
WARNING: F-1(x) does not equal to 1/F(x)
F-1(x) undoes whatever F did.
EXAMPLE: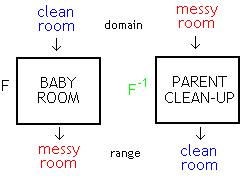
This example is about Mr. K talking about his little girl. When she was younger, they had a play room for her to play in. They had blocks in a box that was all neat and tidy. They had another box of stuff animals that are neat and tidy. They had books of a shelf arrange from big to small, hard cover to soft cover. One day, Mr. K's little girl would go into the play room and mess everything up. Everything would end up scattered all over the floor. As it turns to night, Mr. and Mrs. K cleans up the play room. The following morning, his daughter would go back to the play room and mess everything up all over again. And when night comes, Mr. and Mrs. K cleans the room once again. Mr. K gave us an example of an inverse. Baby mess up clean room, then parents clean up messy room to become a clean room.
GET IT? GOT IT? GOOD (:
Inverses Considered Numerically:
As ordered pairs: given any ordered pair (a, b), it's inverse is (b, a).
As a table of values: given any function defined by a table of values in x and y. The inverse function has a table of valies where the inputs and outputs are exchanged:
Inverses Considered Symbolically (as equations):
method #1 - algebraically: given any function in x and y, to find the inverse exchange the x and y variables and solve for y.
EXAMPLE:
y=2x3-4
to find F-1..
x=2y3-4
x+4=2y3
x+4/2=y3
cube root x+4/2=y = F-1(x) (SORRY, i don't know how to put the cube root thingy for the whole thing =/).
method #2 - conceptually: given any function F to find the inverse list the operation applied to F, then rewrite them undoing each operation in reverse order.
EXAMPLE: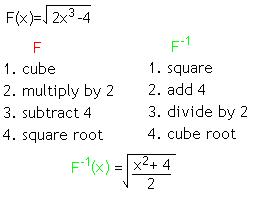
Inverse Considered Graphically:
Given the graph of any function you can find the inverse by reflecting it in the line y=x.
Yeah, and that's about it.. Sorry if everything is all ugly/rushed. Because I pretty much just got off from work (10PM). Oh wells, at least I tried. Oh, btw.. the next scribe is cheeks (:
gooday & goodnight.





 Some people in the class when they heard about the absolute value function were stunned, because they had not heard of this function before, or maybe they've heard of it,but just forgotten. So a little explanation of an absolute value is basically, whatever is inside the absolute value brackets, tells how far away from zero you are. For example:
Some people in the class when they heard about the absolute value function were stunned, because they had not heard of this function before, or maybe they've heard of it,but just forgotten. So a little explanation of an absolute value is basically, whatever is inside the absolute value brackets, tells how far away from zero you are. For example:

 Assume this clock is mathematically correct, i.e. 0 is at the right and the hands move around counterclockwise ... What time is it in radian hours and minutes? ;-)
Assume this clock is mathematically correct, i.e. 0 is at the right and the hands move around counterclockwise ... What time is it in radian hours and minutes? ;-)