Scribe Post _Graphing Trigometric Functions_

Hi, I’m Allen, and I am the scribe for today.

Today we just extended our knowledge about

how to graph trigonometric functions.

Mr. K started the class off with asking us

to graph the following trigonometric functions:

1) y=sin2x-1
2) y=2cosx+1
3) y=2sin(Πx)

~*Solutions:*~

1) y=sin2x-1

2) y=-2cosx+1

3) y=2sin(Πx)

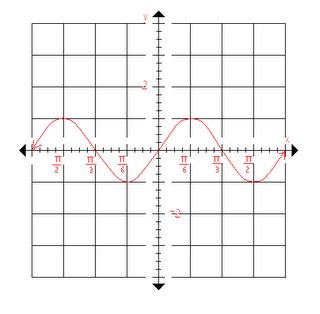
Then we had to graph 2 trigonometric functions with a

phase shift. The questions are as follows:

1) y=sin(x-(Π/4))

2) y=-cos3(x+(Π/6))

~*Solutions:*~

*The way you would graph a phase shift function is to first

draw the graph as if there was no phase shift. So the function

would look like this " y=sinx". Now since there is a -(Π/4) in

brackets beside x the entire graph will move right, NOT left

as the negative (Π/4) suggests.*

1) y=sin(x-(Π/4))

2) y=-cos3(x+(Π/6))

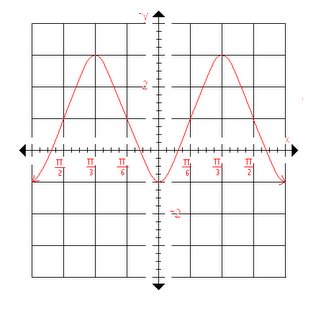
After that we where given a graph and was asked to give at

least 1 cos and 1 sin equation that would results in the

following graph:

~*Solutions:*~

The easiest way to solve a problem like this is to find the values

in the formula "A sin B (x-C)+D" so A, B,C and D. But first you

must choose a point to start from.

-Example1: for sin if I chose the spot where the line intersects

the y axis.-

A=2 because the graph shows the min and max is 2 units up and

2 units down.

B=4 because the graph shows that there are 4 waves in 2Π

(you find this by using the formula "period=(2Π)/B" and if

you put 4 in the result is Π/2 which is the end of 1 wave.

C=Π/8 because this is the phase shift the graph would

undergo to result in its current form if I was looking at it as

a sine value.

D=1 because the horizontal plain where the min and max are

equal occur at positive 1 on the y axis.

So the Final answer would be:

2sin4(x-(Π/8))+1

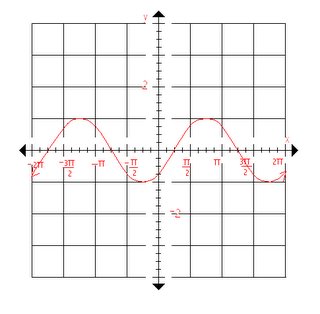
-Example2:for cos if I chose the spot where the line intersects

the y axis.-

A=-2 because the wave starts from its min where it intersects

the y axis. Which is down 2 from the horizontal plain where the

min and max are.

B=4 because the graph shows that there are 4 waves in 2Π
(you find this by using the formula "period=(2Π)/B" and if
you put 4 in the result is Π/2 which is the end of 1 wave.

C=0 because I chose the point where the line intersects the y

axis. Which happens to be the min so no phase shift has occured

(only in the way I choose) ,resulting in a normal cos function.

D=1 because because the horizontal plain where the min and max are
equal occur at positive 1 on the y axis.

So the Final answer would be:

y=-2cos4x+1

*Note* that these are only 2 out of a possible

infinity answers. There areinfinity answers

because each point where the wave reaches i

ts max or min has its own set of A,B,C,&D

combos and since the wave keeps going and

going ( Ill stop there because I may get fined

or something for copying energizers saying.),

but all the equations would be the same becuase they

are on the same wave!!.

Thats all for now, and now for the

moment you've been waiting for

the next scribe will be Anh!!!

And my brother choose this name

so dont get mad at me!