Hi guys its me again!! I hope everyone is enjoying their evening... so
Hi guys its me again!! I hope everyone is enjoying their evening... so
this is what we did today in class.....
We started class off by going over some of the things we did last
Thursday, so Mr. K wrote these on the board.
(a+b)^0 = 1
(a+b)^1 = 1a+1b
(a+b)^2 = 1a^2+ 2ab+1b^2
(a+b)^3 = 1a^3+ 3a^2b+ 3ab^2+ 1b^3
(a+b)^4 = 1a^4+ 4a^3b+6a^2b^2+4ab^3+1b^4
1
11 1
11211
1 13 131 1
11 4 16 14 11
1115110 10 15 11
oCo
Co 1C1
2Co 2C1 2C2
3Co 3C1 3C2 3C3
4Co 4C1 4C2 4C3 4C4
5Co 5C1 5C2 5C3 5C4 5C5
Do you remember those... if you don't you might want to
check
Ashley's lovely scribe post from yesterday for referenceAfter he finished putting all of these back up on the board, we went
over patterns that we fount yesterday like:
Powers of 2
1 1 1 1 2 1 1 3 3 1
1 4 6 4 1 1 5 10 10 5 1
2^3 = 8 111111111111+3+3+1= 8
2^4 = 16111111111+4+6+4+1= 16
And powers of 11
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
11^2 = 121
11^3 = 1331
11^5 = 161051
Whoa that doesn't look
the same... well it still works, you just
have to make sure to do the carrying.
The 5 turns into 6 and the tens turn
into 0 and 1 because 10 carry the 1
leave the 0, and 11 carry the 1 and
leave 1 behind and that 5+ the carried
1 = 6
Ok now here's the new pattern that Mr. K showed us... it shows the
Fibonicci numbers in Pascal's triangle (even though it wasn't pascal
who made it :P )
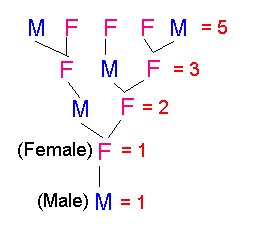
Pay attention cause its hard to see at first!!
The fibonicci numbers can be found on the diagonal edges... the numbers that are cut by this line are added together to show these fibonicci numbers.

Can you see the diagonal edges... they are the pink lines.... the first line crosses through only 1... the next crosses only 1... the next passes through 1 and 1... add these together to get 2... the next row passes through 1 and 2.. add these together to get the 4th fibonicci number 3... and on and on

Can you see it?? if not feel free to come and ask me in class, i'll do
my best to show you and make sure you understand.
After everyone found this pattern Mr. K wanted to point out other interesting
facts... so he told us to take out our calculators...
if you take one fibonicci number, and divide it by the fibonicci number before
it, you will find that as you travel down the triangle, the values get closer and
closer to the "
GOLDEN RATIO" or PHI !!! ∅(phi) =
1.61803399
1/1 = 1
2/1= 2 Can you see how the numbers seem to be
3/2= 1.5 converging (narrowing down) to a single value?
5/3= 1.6667 All getting closer and closer to ∅!!
8/5= 1.6
13/8=1.625
As I've already mentioned, ∅ is the
GOLDEN RATIO... but why is
this so you ask... well because if an item has a ratio that is equal to, or
close to ∅ than it just looks better... unexplainably but it really does..
For example have you ever wondered why 4 by 6 pictures look better
than 5 by 7s... they're smaller, yet they look better... this is because
6/4 = 1.5 * because this has a ratio closer to ∅ it is more visually appealing*
7/5 = 1.4
Another example of this is the Parthenon. This is a temple in Greece dedicated
to the goddess Athena (who is the goddess of wisdom). This temple is also
known as 1 of the 7 wonders of the world as it is one of the most visually
appealing structures in the world. This is because if you look at the Parthenon
it is constructed of rectangles. If you take the larger length of each rectangle and
divide it by the shorter length you will find that the ratio is 1.618... or really
close to the GOLDEN RATIO !
Everything is connected!!! The Fibonicci ratio is not only encoded Pascal's
Triangle, but it is also in various aspects of life, including the human body.

This is the Vitruvian Man done by Leonardo Davinci. (Found on Flickr,
posted by absolutesteven) It is known as the most accurate drawing of
a human being ever done. Why is this... i bet you can guess... that's right
Davinci made sure to measure every and make sure that every
part came out close or equal to the
GOLDEN RATIO ....
ex.
Man's height / distance from ground to navel
Man's arm / distance from elbow to tip of middle finger
Don't you just love it when everything fits together like that?? :D
After his speech on the GOLDEN RATIO, Mr. K brought us back to
the (a+b)^x expansions....
What are the patterns???
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
oCo
1Co 1C1
2Co 2C1 2C2
3Co 3C1 3C2 3C3
4Co 4C1 4C2 4C3 4C4
5Co 5C1 5C2 5C3 5C4 5C5
Firstly the co-efficents for the expansion can be found within
the triangle (look at above triangle with matching colour)
(a+b)^4 =
1a^4+
4a^3b+
6a^2b^2+
4ab^3+
1b^4
Can you see the co-efficents??
1, 4, 6, 4, and 1
according to the 5th row
and 4Co row...
tells us the exponents for the expansion
a^(e-x) b^x
e = what it is being chosen out of.. in this case 4
4Co 4C1 4C2 4C3 4C4
so this expansion is
a^(4-0) + a^(4-1) b^1 + a^(4-2) b^ 2 + a^(4-3) b^3 + a^(4-4) b^4
a^4 + a^3b + a^2 b^2 + a b^3 + b^4
If you add these two patterns together you will get...
1a^4 + 4 a^3b + 6a^2 b^2 +4 a b^3 + 1b^4
the expansion of (a+b)^4
Now, if asked to find the 3rd term of (a+b)^4 do you have to
figure, and write out the whole expansion. Sure why not,
(a+b)^4 is easy... but what if i asked for the 7th term of
(a+b)^11?? do you really want to write that out??
I can guess that your answer, like mine, is NO WAY!!!
Ok now its time to show you how to do this much QUICKER
and much EASIER....
First of all i must make sure that it is clear to you that as we go along
the triangle from the left to right the terms are numbered from 1
increasing... 1, 2, 3, 4, 5 etc.
oCo
1Co 1C1
2Co 2C1 2C2
3Co 3C1 3C2 3C3
4Co 4C1 4C2 4C3 4C4
5Co 5C1 5C2 5C3 5C4 5C5
11112222333444455556666
So,
5Co is term
15C1 is term
25C2 is term
35C5 is term
6
Do you see the pattern, the term number is always 1 larger
than the amount being chosen!!
Therefore, if the number being chosen is always 1 larger,
when we ask for the Xth term, we must subtract 1 so it will
look like this nC(x-1) where n equals the amount being
chosen from.
Ok given this question, 7th term of (a+b)^11
lets use what we know, and the new equation
11 is the number being chosen out of and takes the place of
the n. looking like this 11C(x-1)
7 is the term we want, and takes the place of x.
looking like this 11C (7-1)
Do the math... 11C6 is what you are left with. Now use
rules from before that state that give exponents to a and b
a^(e-x) b^x
e = what it is being chosen out of.. in this case 11
b = the number chosen, in this case 6
a^(11-6) b^6
a^5 b^6
Now put both portions together!!
11C6 a^5 b^6
This will be the 7th term in the expansion of (a+b)^11
Lets try this again to make sure you've got
it....
find the 5th term of (a+b)^13
13 is amount being chosen from
5-1 = 4 this becomes the number being chosen!!
Therefore this becomes 13C4
next comes the exponents
13-4 = 9 which becomes the exponent on a
4 is the exponent on b
put them together
13C4 a^9 b^4
is the 5th term of (a+b)^13
Mr. K tested the class a few more times, and soon a couple
people could find the Xth term of an expansion in less than
10 seconds, and the rest of the class could do it in under
30 seconds.... can you?? Time yourself... If you work at
it you'll get there... if you have any questions just ask me
i'm always willing to help if i can!!
Ok guys time to turn up the heat!!
How many terms are in each expansion?? How do we know this??
Well the number of terms in an expansion can be found by taking the
power of the expansion...
ex. (a+b) ^11
the power is 11
take this power and add 1
11+1 = 12
12 is the number of terms in the expansion!!
What would happen if we were asked to find the middle term of the
expansion??
for odd numbers this is easy, all you need to do is add 1 to the power,
then divide by 2
13 +1 = 14 14/2 = 7
Therefore the middle term in this expansion is the 7th term!!
* this formula will only work if the power you start off with is odd*
In order to find the middle term for an even power, we take the
power, divide by 2 and add 1
12 / 2 = 6 6+ 1 = 7
Therefore the middle term in this expansion is the 7th term!!
* this formula will only work if the power you start off with is even*
Now that we can find the middle term of the expansions we've practiced,
can we find the middle terms of other binomial expansions??? YES!!!
how about [x-(2/x)]^7 ?? what is the middle term of this??
First of all lets make this into something we can understand shall we??
Let a = x
Let b = - 2/x to make this even simpler we're going to change
this into - 2x^(-1)
so now the binomial looks like this
(a+b)^7 and that is much better....
now find the middle term... 7 is odd therefore we must add 1 to make 8 and divide by 2.. the middle term is 4!!
now show the term 4 of this expansion.
7C3 a^4 b^3 *reference above if you don't remember how
1111111111111to do this step*
now rewrite 7C3 in terms of factorials....
7! / (4!3!) a^4 b^3
4! reduces leaving--> 7x6x5 / 3! a^4 b^3
6 and 3! reduce as 6 = 3! leaving--> 7x5 a^4 b^3
35 a^4 b^3
Now substitute the real values of a and b back in.
35(x)^4 (-2x^-1)^3
35 x^4 (-8x ^-3)
-280x^1
therefore -280x^1 is the middle term in the binomial expansion
of [x-(2/x)]^7
Lets try this again to make sure you've got it!
Find the middle term of (x^2 - 2/x)^8
now make this simpler for yourself
Let a = x^2
Let b = -2/x even simpler -2x^-1
now the binomial looks like
(a+b)^8middle term for the power of 8 is the 5th term
therefore 8C4 a^4 b^4
write in terms of factorials
8! / (4!4!) a^4 b^4
4! reduces leaving--> 8x7x6x5 / 4! a^4 b^4
Now substitute the real values back in
70 (x^2)^4 (-2x^-1)^4
70 x^8 (16x ^-4) 111
1120x^4 1111111111
1111111111111111
A common mistake made is when the exponent
is an even number, the student forgets to make
the coefficient positive. Watch for this!!
Therefore 1120x^4 is the middle term in the binomial
expansion of (x^2 - 2/x)^8
CONNECTIONS ARE EVERYWHERE!!!!!!
As you have seen through class and scribe posts for this
unit, everything is connected and therefore
Combinations and binomials go hand in hand!!
The last of the class was spent reviewing most of the above one more time, in order to really make sure that we understood!!
I hope everything in this scribe post is useful to you. If you have any questions or concerns don't hesitate to ask me, I'm here to make this scribe post make perfect sense to you!! Enjoy the rest of your evening, and i'll see you all tomorrow!! Good Night!!
p.s please make sure to have at least 5 pictures on your flickr account if you are a new user. If you do not, your account will not be reviewed, and therefore not deemed safe to make your pictures public for the assignment!!
Oh ya... and just to finish this off, jessiccal_198 your scribe tomorrow :)
Ok i believe that the spacing is fixed now... see you later!!