6th Scribe Post: Quiz 1 on Circular Functions

Hi everybody!! I'm Ashley and I'm the scribe for today's blog! At the very beginning of class there wasn't much talk about math which is a good thing for me. I don't have to write down as much. Mr.K basically said from what I heard is that you should not reveal personal information on the internet. He stresses no last name should be shared and that we should read the post "Student's made this" because it's very important. Another thing he said was that to post a blog you should go to beta.blogger.com and sign in there to post. So after he went on about the blog he revealed that there will be a quiz. I was in complete shock but then I remembered him saying that yesterday so it wasn't a total surprise.
The quiz was called Quiz 1 on Circular Functions and these are the questions(blue) and answers(red):

1) Convert the following to radian measure, expressing your answer in terms of Π. (2 marks each)

(a) 25°
180°/Π = 25°/θ
180θ = 25Π
180θ/180 = 25Π/180
θ = 25Π/180
θ = 5Π/36

(b) 460°
180°/Π = 460°/θ
180θ = 460Π
180θ/180 = 460Π/180
θ = 460Π/180
θ = 23Π/9
*Remember to add the degrees symbol on your setup because you will lose marks. I think it's -.5 for this question.

2) Convert the following from radain to degree measure. Round your answers to one decimal place where necessary. (2 marks)

(a) -7Π/6
180 º/ Π = θ /-7p/6
-659.7345 = θΠ
-659.7345/Π = θ/Π
-210º = θ

(b) 2.634
180 º/ Π = θ/2.634
474.12 = θΠ
474.12/Π = θ/Π
150.9º = θ
*Remember like in the first question to add the degrees symbol on your setup because you will lose marks. I think it's -.5 for this question as well.

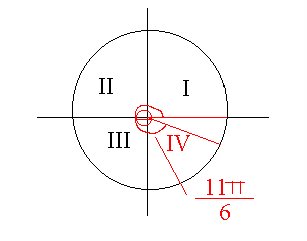
3) Determine the quadrant in which each angle lies. (1 mark each)

(a) 2Π/3

Answer: Quad II

(b) 11Π/6

Answer: Quad IV

(c) -Π/4

Answer: Quad IV

(d) -11Π/6

Answer: Quad I

4) Assuming the point P lies on the intersection of the unit circle and the line segment joining the origin to the point Q(-9,40), find the coordinates of P. (4 marks)

(-9)2 +(40)2 = r2

81 + 1600 = root of 1681

root of 1681 = 41

x/-9 = 1/41 => x = -9/41

y/40 = 1/41 => y = 40/41

Sinθ = 40/41
Cosθ = -9/41
P θ = (-9/41,40/41)
*Remember if you draw a diagram you must correctly place the angle in the right place on the circle. For this question you would have lost 1 mark. Another thing is to add the equal sign where needed because you will lose marks and to correctly place the x and y coordinates in the answer.

After the quiz he collected it and randomly gave us other people's quizes. He told us how to correct it and where we would lose the marks.
You would lose marks in the following:
- Not adding the degrees symbol
- Incorrectly placing an angle on a diagram
- Not placing the equal sign on your work
- Incorrectly placing the x and y coordinates in the answer for example if the answer was Pθ=(9,40) but you put Pθ = (40,9).
There's more but I can't remember them but you get the idea right? The setup should always be correct because it's not only about the answer but the steps you take to get to the answer is important too.

I'm not done yet so bare with me. Just before the bell rang Mr.K wrote on the board
5x - 3 = 4x + 16
5tanx - 3 = 4tanx + 16
tanx = 19
He then told us we were looking for the arc tangent of 19 and told us to punch in 2nd function tangent then 19 into our calculators. The answer became 86.7º which we round off to 87º. We know that 87º is in quadrant one but wait there's a second answer as well.
Remember that sinθ maximum is -1 and 1 and cosθ maximum is -1 and 1 as well but tanθ has no maximum. So there will always be two answers. To find the second answer remember that in Quadrant I, tanθ is positive but in Quadrant III tanθ is positive as well. So you would have to add 87º after Quad II which will look like this:
87º + 180º = 267º which brings you to Quad III.

So that's it for me. Yay! If there are any mistakes please comment okay because I'm still new to this and this is my first post. Bye for now!

Oh by the way the next scribe will be........ hellochipsahoy