Scribe Post: Translations & Reflections

Hello everyone! I'm Jess and i'm the scribe for today's class. At the begining, we started with three questions about the transformations that we have learned yesterday. And here's the questions:
1. f(x) = x^2 ; Sketch f(x-3)+2

*As we know, -3 is C => shift to the right 3 units, and +2 is D (the last part of the function) => shift up 2 units, and we get the new vertex at (3,2)

2. The graph of g(x) is formed by sliding f(x) 4 units to the left. If f(x) = sin(x+2)-5 ; write the equation of g(x)

g(x) = sin(x+6)+5

*because f(x) moves 4 units to the left to get the graph of g(x), therefore it becomes 6

(x+2) = (x-(-2)) => (x-(-2)+(-4)) = (x-(-6)) => (x+6)

3. Below is the graph of y = f(x)

a. 2f(x) b. f(2x) c. 2f(x)-1

Here's all the graphs for the all the functions above:

a. for this question, we're doubling the y-coordinate
(-1 , 3) => 3(2) = 6 therefore we get the point (-1,6)

(-3 , -2) => (-2)(2) = -4 ; we get the point (-3,-4)

(4 , -1) => (-1)(2) = -2 ; we get the point (4,-2)

* in this one, 2 does not affect the x-coordinate

b. for this question, we're doubling the x-coordinate

(-1 , 3) => -1(1/2) = -1/2 therefore we get the point (-1/2,3)
(-3 , -2) => (-3)(1/2) = -3/2 ; we get the point (-3/2,-2)
(4 , -1) => (4)(1/2) = 2 ; we get the point (2,-1)
* in this one, 2 does not affect the x-coordinate

On the other note, in grade 12, we only deal with multiplication and addition, and we dont use division or subtraction.

Examples: instead of divide by 2, we multiply 1/2, and instead of subtract, we add the negative number of that number!

c. for this question, the function 2f(x)+1, both numbers affect the y-coordinate
(-1 , 3) => 3(2) = 6, then we shift 1 unit up => 6+1=7 ; therefore we get the point (-1,7)

(-3 , -2) => (-2)(2) = -4 ; shift 1 unit up => -4+1=-3 ; we get the point (-3,-3)

(4 , -1) => (-1)(2) = -2 ; shift 1 unit up => -2+1=-1 ; we get the point (4,-1)

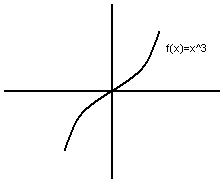
Moving on, Mr. K started with a new function f(x) = sin(x)

if we change f(x) to -f(x), then we'll get -sin(x) => -f(x) = - sin(x)

and if we multiply f(x) by 2, the graph will stretch by 1/2

if we change f(x) to f(-x), it will flip over the y-axis

from here, we come up with f(-x) = -f(x)

f(-x) = -f(x) This is called the definition of an odd function

The graph above is an odd function since if we flip it over the y-axis, we'll have a different graph.

Start with a new function, g(x)=x^2

- if we change g(x) to -g(x), instead of open up, the graph will open down

- if we change g(x) to g(-x), the function will flip over the y-axis, in this case, there's nothing change, the graph remains the same, from here, we come up with g(x) = g(-x)

g(x) = g(-x) This is call the definition of an even function.

*even function : no changes are made in the graphs

From those graphs above, we have 2 cases:

even function, g(x) = g(-x) and odd function, f(-x) = -f(x)

*Most functions are not odd nor even function.

Reflection:

- to reflect the x-axis, change the y-axis

- to reflect the y-axis, change the x-axis

Like Mr. K said, we still have one more type of transformation or function to talk about but since there wasn't enough time, so we'll leave it for tomorrow's class!
By the way, this is my first scribe post and it took me awhile to get this done, so hopefully, everyone understand it and if not, you know who you can look for help! And please do comment if i got anything wrong! Have a nice day everyone!

Oh and the next scribe post will be... japs_world. Good luck!