Scribe, Problem solving

In morning's class we talked about the equation , how it can't be zero: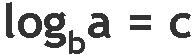













Mr.K explain why it can't be zero. Well 0⁰ doesn't not exist. That being zero can
never happen Because it can never touch the x-axis.Also it's undefined.




continuing from last Math dictionary


Example: Gerald invested $600 at 8% interest, compound semi-annually
How long will it take for his investment to double?


Solution: A=P(1+c/n)<sup>cn

A: 1200
P:600
r:0.08
n:2
t:???


1200 = 600(1+0.08/2)2t
2=(1.04)2t
ln2 = 2t ln(1.04)
ln2/ln(1.04) =2t
(1/2 )ln2/ln(1.04) =t
8.8365 year = t


it would take 8 years or 10 months


How we got 10 month is:
8.8365 x 12 =10.0379</sup>


Common logarithm
The base 10 is used so frequently with logarithms that it is known as the "common logarithm".
when the base of a logarithm is not indicated , base 10 is assumed.


i.e. log10^x = logx


Natural logarithm
e = 2.718281828459
e(Euler's number) is a number that a rises naturally in the logarithmic functions;
Partcularly in the case of coutinuous expontential growth ( or Decay)
The natural Log arithm is typicallu written as lnx;read as "Ellen of x"

ie loge^x = lnx


<sup>Exponential modeling
The basic function: f(x) =abx
how we model real life situations depends on what kind, or how much , information we are given:


case 1:
Working with a minimal amount of information(A,Ao, (Tri)t) we will create a model in base 10 and base e... base e is prefered.

A= Ao(model)*

A0: is the original amount of "substance" at the beginning of the time period.
A: is the amount of "substance" as the end of the time period.
Model: is our model for the growth (or decay) of the substance", it is usually an exponential expression in base 10 or base e although any base can be used.
t: is the amount of time that has passed for the substance" to grow(or Decay) from A0 to A.


example:
The population of the earth was 5 billion in 1990. In zool it was 6.2 billion.
a. model the poplution growth using an exponential function.
b.What was the population in 1999?

a.
A:6.2
A0: 5
(tri)t= t= 2001 -1990= 11

A=A0(model)t
6.2 = 5(model)11
The are two ways , but the same answer.

Base 10

Log(6.2/5) = log(model)11
log(6.2/5)= 11 log(model)
(1/11)log(6.2/5)=log(model)
0.00849 = log(model)
100.00849 = model

A=5(100.00849)
A= 1.0197

Base e

ln(6.2/5)= ln(model)11
ln(6.2/5) = 11 ln(model)
(1/11) ln (6.2/5) = ln(model)
0.01956 = ln(model)
e0.01956 = (model)
A= 5e0.01956t
e= 1.0197

b.
t = 9 in 1990 - 1999
a(9)= 5(100.00849(9))
=5.9622

A(9)= 5e0.01956(9)
=5.9622


Case 2: Given lots of information (A0,M,P)
A=Aom(t/p)

A: is the amount of "substance " At the end of the time period
A0: is the original amount of "substance" at the beginning of the time period.
M: is the "multiplication factor"or growth rate.
P: is the period; the amount of time required to multiply by "m"once.
t: is the time that has passed.


Example:
A colong of bateria double 6 days. If there were 3000 bacteria to begin with how many bacteria will there be in 15 days?

A=
A0=3000
M=2
P=6
t=15

A=Aomt/p
A=3000(2)15/6
A=16970.5628
There will be approximately 16971 Bacteria


At the end of the period there were three questions.


1. You have $10,000 and invest it all at 12% compounded quarterly
how long will it take you to become a millionaire?.


2. It is estimated that 20% of a radioactive substance decays in 30 hours
what is the half life of this substance?.


3.The population of toronto was 4000,000 in 2000. The growth is modeled by P(t) = 4000,000 e0.012t what year will the population be 6,400,000?.


.OOOO SNAP!!!!! XD
.
.

Next scriber is daphne</sup>