Permutations and Combinations

Permutations and Combinations

Hey guys, it's James! My turn today to scribe, sorry I am posting so late, it was due to

work. I'll try to get it done by tonight, if not tomorrow afternoon :).

For a heads up, the next scribe will be Gerald tomorrow.

SORRY I'LL MAKE IT LOOK NICE TOMORROW! IM TIRED ;)

Today we went more thorough in our new unit of Permutations and Combinations AKA Principles

of Counting. We started off doing 3 questions...

1) How many different sandwiches can you make given 5 choices of meat and 4 different types

of bread. (Each sandwich can have only one type of meat.)

2) A License plate is made up of 3 letters followed by 3 digits. How many different license

platers can be made?

3) How many positive odd integers can be formed, less than 10,000 using digits...
a) 2, 3, 4, 5, 6
b) 3, 4, 6, 8, 0

*Also find the positive even integers*
*AND also find them if integers can't be repeated*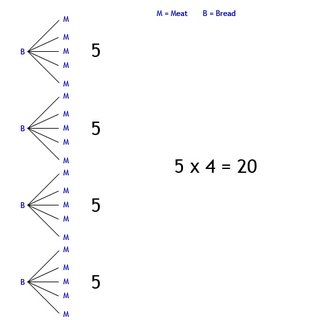


*IMPORTANT* One thing to keep in mind when identifying a question is to make sure that you

look to see if it's restricted or not. What I mean by this is if you can repeat variables.

(ex. integers, letters, living/non living, etc.) I'll explain as I go along!

We first warmed up with one of yesterdays kind of questions...

1) How many different sandwiches can you make given 5 choices of meat and 4 different types

of bread. (Each sandwich can have only one type of meat.)
Start off by identifying what's given to you.
Meat = 5
Bread = 4

5 x 4 = 20
Therefore there are 20 types of sandwiches that can be made.

Here's an example...



2) A License plate is made up of 3 letters followed by 3 digits. How many different license

platers can be made?
*IMPORTANT* This is a question that may have a restriction.
Identify what is given.
You have 6 spots, 3 for letters and 3 for digits.

*NOTE* An easy way for you to do most questions is to draw out the spots like shown.

_ _ _ _ _ _
A A A # # #

'A' represents a letter
'#' represents a digit

To figure out this question(keeping in mind you can repeat letters and digits) find out how

much letters/digits a spot can hold.

_ _ _ _ _ _
26 26 26 10 10 10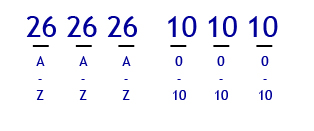


With all the information plugged in, just multiply all numbers together and you will have the

answer.

26^3 x 10^3 'or' 26 x 26 x 26 x 10 x 10 x 10 = 17,576,000
Therefore there are 17,576,000 ways to make a license plate.


3) How many positive odd integers can be formed, less than 10,000 using digits...
a) 2, 3, 4, 5, 6
b) 3, 4, 6, 8, 0
*IMPORTANT* Again this is a question that may have restrictions. For each question, I will

show you how to do each.

a) First off identify what is given.
- You have 5 integers
- It must be less than 10,000 so that gives us 4 spots
- It must be positive

***ODD***
_ _ _ _
5 5 5 2

How did you do this? Let me explain, with 4 slots draw them out. You now know that you have 5

integers you can choose from. First slot, you can put any 5 integers there, with the second

and third you may do the same because numbers are not restricted in this one. BUT, for the

fourth slot you must put 2. Why? Because I SAID SO! Kidding :P The reason is, is because your

answer has to be an odd number, to make the result an odd number all you need to do is plug

in the odd integer, which in this case is '3' or '5'.

5 x 5 x 5 x 2 = 250 ways to make an odd number

***EVEN***
_ _ _ _
5 5 5 3

Just like the ODD way to do this, the even way is very similar without using restrictions.

Instead of making the number odd, we will make it even. Within this question, we have 3 even

numbers, this results in the fourth slot being 3.

5 x 5 x 5 x 3 = 375 ways to make an even number

***RESTRICTED ODD & EVEN***
_ _ _ _ ODD
4 3 2 2
_ _ _ _ EVEN
4 3 2 3

Confused?? Well it is a bit confusing at first, but let me explain.
Restrictions means that a variable can not be repeated. with the 5 integers given, 1 integer

can only be used once in the slots.

We'll look at the odd first...
Best thing to look at is the fourth slot, you still need to make it odd, so you plug in the

integer 2.
_ _ _ _
? ? ? 2
Now look at the first slot, with one integer now chosen because of the fourth slot, you now

have 4 out of 5 integers to work with. So plug in 4.
_ _ _ _
4 ? ? 2
The rest gets easy from here, with now 2 out of 5 integers chosen, you have 3 left. Guess

what number should go in the second slot? You're right, it's 3!!
_ _ _ _
4 3 ? 2
I'm sure you can figure out the third slot.
_ _ _ _
4 3 2 2

4 x 3 x 2 x 2 = 48 ways to make an odd number without repeating integers.

When even, it is pretty much the same procedure. So I won't type out all the steps again,

just the answer.
_ _ _ _
4 3 2 3

4 x 3 x 2 x 3 = 72 ways to make an even number without repeating integers.

b) Tired of reading? I'm sure some of you are :P.
First off lets identify what is given.
- You have 5 integers
- It must be less than 10,000 so that gives us 4 spots
- It must be positive
Same concept as what we did in (a), BUT now we have a 0 integer.

***ODD***
_ _ _ _
4 5 5 1

We only have 1 odd integer so we can plug it in at the last spot. Since it is like (a) we can

just plug in 5 for the first spot right? WRONG! Since we have a 0 in this one, a number can

never start off with 0. So we can use 4 out of 5 integers, so plug in 4. Now for the second

and third, we can use the integer 0. So we have 5/5 integers to choose from. So...

4 x 5 x 5 x 1 = 100 ways to make an odd number.

***EVEN***
_ _ _ _
4 5 5 4

The Same concept yet again, follow the steps I just typed out :P

4 x 5 x 5 x 4 = 400 ways to make an even number.

***RESTRICTED ODD & EVEN***
_ _ _ _ ODD
4 3 2 1
_ _ _ _
4 3 2 1
_ _ _ _ EVEN
3 3 2 3

OH NOES! More confused? Don't worry, it's not as hard as it looks.

*NOTE* '0' Is really important in this kind of question. Since it is an even number it will

not effect the restricted odd way to do this at all.

From question (a) the odd will be pretty much the same! But with 0 in mind, 0 still cannot be

the number in the first slot. So this results in...
_ _ _ _
4 3 2 1

4 x 3 x 2 x 1 = 24 ways to make an odd number without repeating integers.

PHEW!!! Okay, you've come this far... Now for the big stuff!

The reason I posted two ways is because there are two solutions due too the number '0'.
First solution is...
_ _ _ _
4 3 2 1
This is the first solution, to get this solution the fourth slot must be 0. You may then plug

in the rest of the 4 numbers for slot 1. 3 numbers for slot 2 and 2 numbers for slot 3.

4 x 3 x 2 x 1 = 24 ways to make an even number without repeating integers.

The second solution is...
_ _ _ _
3 3 2 3
The second solution is the result of the fourth slot NOT being 0. Since we have 4 even

numbers(4, 6, 8, 0), take out the '0' and you will have 3 in the fourth slot. For the first

slot you will now have 4 numbers(including 0). Since 0 cannot be the first slot, you take it

away and it will result in 3. For the second slot, you may add 0 back which will leave you

with again 3/5 integers. So the second slot is 3. Third slot is a given with 2 integers left.

3 x 3 x 2 x 3 = 54 ways to make an even number without repeating integers.


BONUS QUESTIONS.
How many ways can you arrange the letters in this word to make other words. (Imaginary words)
a) T A L K

b) B O O K

c) M I S S I S S I P P I

a) T A L K
T = 1
A = 1
L = 1
K = 1
Therefore 4! 'or' 4 x 3 x 2 x 1

b) B O O K
B = 1
O = 2
K = 1

*NOTE* Though you can write out every way to write the the word book. It will look really

weird and will result in double words because you have to alternate the 'O's'. Instead of

doing that we can just use the equation.

4! -> Number of Letters
-
2! -> Number of Duplicates

Therefore the answer is 12.

c) M I S S I S S I P P I
M = 1
I = 4
S = 4
P = 2

11! -> Number of Letters
-
4!4!2! -> Number of Duplicates



Well this is the end of my scribe post, I look forward on doing my next one!
Again the next scriber will be Gerald!

Thanks!
- James