Counting Problems
Okay, today Mr.K explained more about the online assignment we had to do on the Flickr site. For anyone who wasn't in class, you have to get one picture that represents something of Trigonometry. It has to be in the real world, not something drawn up and then photographed, but you can also set it up how you want it to be. Just remember it has to be a trigonometry picture; it could represent a triangle, a sine graph, angles, area, degrees, etc. When you get your picture try to incorporate as many different concepts of trigonometry as you can. After showing us he went to putting up the questions on the board.
- From a 52 card deck, how many 5 card hands have:
a) 3 hearts and 2 clubs?
b) 4 of a kind (4 cards, same face value, and 1 card of a different face value)
c) Royal flush (A, K, Q, J, 10, with the same suit)d) straight flush (5 cards, in sequence, of the same suit)
2) Find the 6th term of (x - 2y)^9
3) Find the middle term of (3a + 2b^2)^6
4) Which term of (x^2 - 1/x)^6 is constant?
The Answers:
1. a) 13C2 . 13C3 = 22 308
b) First we got the total number of hands dealt
52C5 = 2 598 960
13C1
We get this value because of the 13 different face values
4C4
We get this value because there are four suits in each face value, and since we need four ofa kind it's 4C4.
12C1
Since this choice is supposed to be a different suit then one of the face values will be eliminated
4C1
We only need one of the face values and only one suit.
Afterwards we just multiply it all together:
13C1 . 4C4 . 12C1 . 4C1 = 624
c) The answer would be:
1 . 4c1
There reason we are multiplying 4c1 by 1, is because there is only one way to get the sequence
4C1 just means that it could be any one of the 4 suits.
d) This one is different because you don't count the royal flush.
This problem is also related to a problem we did in previous classes, where there were 4 students and 9 seats to fill.
the answer would be:
9 . 4C1
Because there are nine different ways to get the sequence, and 4C1 means that the whole had has to be one suit.
2) To find the sixth term of (x - 2y)^9, you have to remember that 9C0 also counts as a term.
Solution:
9C5 (x)^4 (-2y)^5 = 126 x^4 (-32y^5)
= -4032 x^4 y^5
3) Let x = 3a y = 2b^2
6C3 x^3 y^3 = 20 (3a)^3 (2b^2)^3
= 20 (27a^3) (8b^6)
4) 1st term:
6C0 (x^2)^6 = x^12
2nd term:
6C1 (x^2)^5 (-x^-1)^1 = x^9
3rd term:
6C2 (x^2)^4 (-x^-1)^2 = x^6
...
The 5th term is the constant term.
6C4 (x^2)^2 (-x^-1)^4
= 15 <--- This is the value for the constant term
(a + b)^p
pCd (a^c) (b^d)
c + d = 6
2c - d = 0

SECOND CLASS...
- (2x^3 - 1/x^2)^10 Find the constant term
- The 4th term of (x - 1/2)^n is -15x^7, find n.
- How many ways can a person get from point A to B?
4. In a 52 card deck, find the number of ways to get a 5 card hand that is:
a) a full house (3 cards of one face value, 2 of another)
b) Flush (5 cards, same suit, not in sequence)
c) Straight (5 cards in sequence, not all the same suit. Ace high or low)
d) 3 of a kind
e) Two pair
f) One pair
g) No pairs
10C6 a^4 b^6
10!/(6!4!) (2x^3)^4 (-x^-2)^6
210 (16x^12) (-x^-12)
3360
An extra question...Find the term that contains x^15
10C7 (2x^3)^7 (-x^-2)^3
-120 (128x^21) (-x^-6)
-15 360 x^15
2. nC3 a^(n-3) b^3 - - 15x^7
n!/((n-3)!3!) (x)^(n-3) (-1/2)^3
x^(n-3) = x^7
n-3 = 7
n= 10
3a) The answer is
7!/(4!3!) = 35
Going right, then down.
We get 4! because you're going RRRR. You're making four rights on the squares.
3! because you're going DDD. You're down 3 squares.
The combination would be RRRRDDD, it's how you're getting from point A to B.
Another way was using Pascal's Triangle:
As you can see, when you look at it at an angle, you can see pascal's triangle.
B) RD = 2
c) RRRRD----5!/4 = 5
d) RRRRDD . RRD . RRDD
6!/(4!2!) . 3!/2! . 4!/(2!2!)
15 . 3 . 6 = 270
4a) 13P2 . 4C3 . 4C2
We used 13P2 because the order does matter.
b) 4C1 . 13C5 - 10.4C2
the 10.4C1 is the total number of flushes in sequence.
Well that's the end of my scribe. I hope it was informative to all of you. The next scribe shall be......Jhoann.




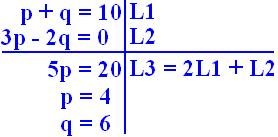
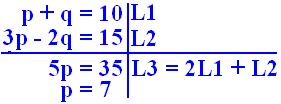


No comments:
Post a Comment