At the beggining of class we were given 9 questions to solve they were seen on the whiteboard like this


We were given time to solve this equations, after the time was done we explained how we got our answers.
Question #1
To find the area of triangle ABC we had to find the points of A, B ,C is this is the step by step solution.
Point A is found by plugging our x value into the equation y=3x, our given value for x was zero(0), and any power to the exponent of 0 will always equal to 1, which gives us the coordinates (0,1) and that is the coordinate for point A
Point B is found by plugging in our x value also into the equation, we got the value of x by the ordered pair below point B which was (2,0), when we plug in the value of x into the equation y=9, so the coordinates of point B would be (2,9)
Point C is found because we are given the x value which is also seen by above in Point B, and the point Below it, because there on the same x distance, but just different y distance,so the x value is 2, and the y distance is going to be the same as point A because it lies on the same height as point A, so the y value is 1, so the coordinates of Point C is (2,1)

So the solution for question #1 is 8 units squared
Question #2
the solution to question # 2 is found by finding the value of base of x, we simplified it into becoming 2³(2x-1)³=5³, it had the same exponents so we dropped them and simplified it to [2 (2x-1)] ³ = 5³, then we simplified it by it equaling 4x-2 =5, we then moved the -2 onto the other side od the equal sign and we get 4x=7, we then isolate the x and get x= 7/4
So the solution to question # 2 is x=7/4
Question #3
It was a homework question for two classes ago. First off we went by re-writing the question into making it look like this 2^x/ 2 - 2^ x= 2^-3, to make the fraction disappear in the equation we multiply by 2 on both sides of the equal sign, therefore the equation will now look liek this 2^x - (2)2^x=(2)2^-3, at this point dont add because you'll end up getting the original equation, so what you do now is solve by factoring. You will isolate the varaible 2^x. So it will be written like this 2^x(1-2)=2^-2, it will then end up like -2^x = 2^-2 , after simplifying. Therefore we concluded there is no solution because even if you were to multiply everything by 1 youll still have a postive power one side, and a negative power on the other, therefore staing its not true.
So the solution for question # 3 is NO SOLUTION
Question #4
When we were asked to simplify (3^ 5)(3^7), we can say that when we are multiplying powers with the same base we add the exponents, therefore it can be simplified by writing it like this 3^(5 +7), in other words 3^12
So the solution for Question # 4 is 3^12.
Question # 5
when we are asked to simplify 5^11/5^4 we can say that when dividing powers with the same base we subtract exponents. If you apply this concept you will get an outcome like this 5^(11-4) or in other words 5^ 7.
So the solution for question #5 is 5^7
Question # 6
When we are asked to simplify (4^3)^5, we can say that when a power is raised to a power we multiply the exponents, so it would look like this [4^(3)(5)] or in other words 4^ 15
So the solution to Question#6 is 4^15
Question 7-9 remember LOGARITHMS ARE EXPONENTS!! BECAUSE MR.K KNOWS THAT AT LEAST 6 OF US ARE GOING TO FORGET. These questions are also for us to adapt on knowing how to run our tools backwards, and fowards.
Question#7
When asked to simplify log2^8 + log2^32, we look at as its adding expoents, so your multiplying powers that have the same bases, so that question can be simplified as log2^(8)(32) or log2^256.
So the solution for Question #7 is Log 2^256
Question #8
When asked to simplify log3^81 - log3^9, we look at it as we are subtracting exponents meaning we are diving powers. Thefore the equation can be written like log3^(81/9) or in other words log3^9.
So the solution for Question # 8 is log 3^9
Question #9
When asked to simplify 2log5^125, we see here that we are going to multiply powers, which can be also known as to raising a power to a power. So it can be written like log5^125^2,or in other words log 5^15625
So the solution for question #9 is log 5^15625.
log a^(mn) = log a ^m + log a^n
log a ^(m/n)= log a ^m - log a^ n
log a^(m^c) = C loga^m
The above was written on the whiteboard after the qesutions were completed. These are the concepts we applied to our questions from earlier to get our solutions.
We were then given some new questions, and we were asked to write them as a single logarithm
The four questions were
a) 1/2 log a^9 - log a^3
simplify the equation as log a^3 - log a^3 which will give us loga ^ 3/3 by the corresponding concept of subtracting exponents meaning your dividing powers, you will then get to simplify as loga^1 which will give us 0.
The solution to a) is zero(0)
b)log a^6 + log a^4
adding exponents is the same as multiplying powers, so therefore it would simplify as loga^(6)(4), which in other words can be loga^24.
The solution to b) is loga^24
c) 2log a^5 + loga^4
simplified as loga^25 + loga^4, then we apply the adding exponents meaning multiplying powers so we simplify it by writing it as log a^ 100.
The solution to c) is loga^100
d) log a^ 6 + log a^ 8 - 1/2log a^16
therefore we simplify the adding of exponents as multiplying powers, and then simplifying the multiplying of exponents as power raised to a power, so it can be rewritten like,loga^(48)-log a^(16^1/2), which then can be simplified as loga^ (48/4), which can even be more simplified as loga^12.
The solution to d) is log a^12
GET OUT YOUR MATH DICTONARIES

NEW PAGE EVERYBODY

Logarithms
Definition:
#1 the logarithm function is the inverse of the exponental function.
#2 the logarithm function is the function that turns powers into exponents.
REMEMBER: A LOGARITHM IS AN EXPONENT!

And thats all for today folks.....and the next scribe is Richard..he knows already =)















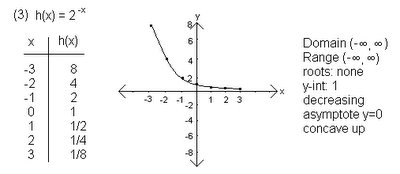
 y = 3^x
y = 3^x next we had to sketch the inverse of the two :
next we had to sketch the inverse of the two : y = 1/(3^x)
y = 1/(3^x)