Saskatchewan Sunrise

To refresh your mind, in my post ill briefly summarize what we had done on Thursdays class. The question was,

For a saskatchewan town, the latest sunrise is on December 21 at 9:15am, the earliest sunrise is on June 21 at 3:15am. Sunrise times on other dates can be predticted using a sinusoidal equation.

NOTE: There is no daylight saving times in Saskatchewan.


a) sketch the graph of a sinusoid described above.


b) write equations for the function; a sine and cosine equation.



c) Use your equation to predict the time of sunrise on April 6.


d) What is the average sunrise time throughout the year?


e) On what days will the sun rise at 7:00am?



Most of the solutions will be found on the graph, so i will show you what we were able to draw from Thursdays graph.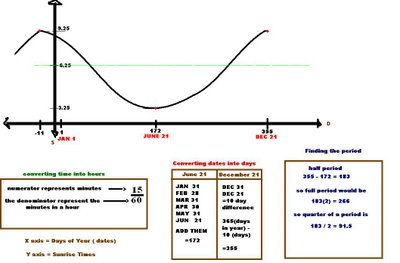








From this graph we completed what was asked in question A, and look at see the solution for D.

d) What is the average sunrise time throughout the year?

SOLUTION:

YOU WOULD ADD OUR MIN. AND MAX. AND DIVIDE IT BY 2.

3.25 + 9.25 = 12.5 / 2 = 6.25


6.25 is also known as our average value, vertical shift and sinusoidal axis

TO CONVERT IT BACK TO TIME IT WOULD BE 6:15 AM.

The average sunrise time throughout the tear would be at 6.15am.





NOW I WILL GIVE YOU WHAT WE WERE ABLE TO FIND OUT FOR FRIDAYS CLASS.

The questions left to answer were B, C, and E.



Looking at the graph we were able to figure out the A( amplitude), B( determining the period), C( the phase shift), and D ( the vertical shift)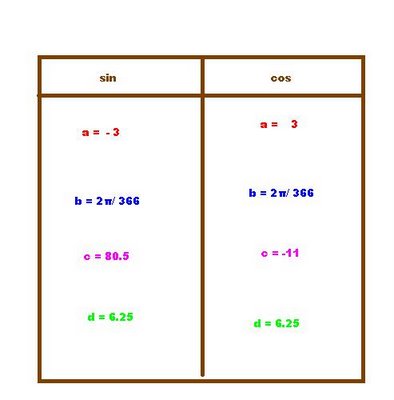




According to this we are able to answer question b.

We just have to plug the A, B, C, D values into the equations needed.

b) Write equations for the function; a sine and cosine equation

SOLUTION:

S(d)= -3 sin[2π/366(d-80.5)] + 6.25
S(d) = 3 cos [2π/366(d-(-11))] + 6.25





Now moving on how to answer question C

c) Use your equation to predict the time of sunrise on April 6.

SOLUTION:
STEP 1: Find out what day of year is APR 6.
ADD THE DATES IN MONTHS
JAN 31, FEB 28, MAR 31, APR 06, = 96TH DAY
the 96 represents our d in the equation which is the day of the year
STEP 2: NOW PLUG INTO YOUR EQUATIONS FROM QUESTION B)
S(96)=-3Sin[2p/366(d-80.5)] + 6.25
or
S(96) = 3 cos [2p/366(d-(-11))] + 6.25

In either equation you use, youwill both get the same answer, which would be 5:28am.

On April 6,we have predicted that the time of sunrise will be at 5:28am.


REMEMBER WE HAVE NEW INFORMATION AND MUST PLOT THESE POINTS ONTO OUR GRPAH THIS IS HOW OUR GRAPH SHOULD LOOK LIKE

Now i will have to discuss and show you how to solve the most complicated question, question E

e) On what days will the sun rise at 7:00am?

If we were to go back to our sketched graph, we would be able to see the appoximate days the sun would rise at 7am. This time we were given the letter S which represent the sunrise time. But we are not given d, which is the unkown value.

(7)(d) = 3cos [2π/366(d+11)] + 6.25

As we look at our sketced graph we will be able to see that the sun will rise at 7am on two days of the year. Our estimations were arund the 70th day and 270th day.

Here i will show you how to figure it out algebraically

Solving with the Sin equation

output should be 7 ( since 7am is the time of sunrise) therefore our equation will look like this

7 = -3sin [2π/366(d-80.5)] + 6.25

[2π/366(d-80.5)] >>>>>>is all some angle so we will,

let ◊ = [2π/366(d-80.5)]

7= -3sin◊ + 6.25

.75=-3sin◊

-0.25=sin◊

WE KNOW SIN IS NEGATIVE IN TWO QUADRANTS SO THE SOLUTIONS WILL BE FOUND IN QUAD III & QUAD IV

arc sin of -0.25 or (sinˉ¹)-0.25 = .252680255

rounded off would be .2527

Mr.K says to round off to 4 decimal places, but when doing your calculations use the whole number from above.

So the solution in Quad IV solution would be -.2527

solution in Quad III would be π + .2527 = 3.9427909

◊ = -.2527 and ◊ = 3.3943

so, [2π/366(d-80.5)] = -.2527

AND

[2π/366(d-80.5)] = 3.9343

Multiplying by the reciprocal will make it easier for us to solve the equation, it will help us by taking out the 2π out of the numerator, and moving it to the denominator.Remember what we do to one side of the equal sign, we must also apply to the other side of the equal sign.

FIRST SOLUTION USING ◊ =-.2527

◊ = [2π/366(d-80.5)] = -.2527

(366/2π)[2π/366(d-80.5)] =-.2527(366/2π)

the (366/2π)(2π/366) reduce each other

so we are left with

d-80.5= -0.2527(366/2π)

d= -0.2527(366/2π) + 80.5

NOTE: BE CAREFUL ON HOW YOU INPUT THIS EQUATION INTO YOUR CALCULATOR

REMEMBER WHEN USING CALCULATOR USE THE WHOLE NUMBER NOT THE ROUNDED OFF NUMBER

ILL SHOW IT TO YOU IN AN UGLY COLOR, SO UGLY COLOR = BAD FOR EYES , AND WHEN ITS BAD , YOU DO NOT WANT TO DO THAT.

Heres a wrong way for this equation to be inputted into your calculator

(-.252680255 ) x (366/2π) + 80.5 = -64.768

it is wrong because in that equation above the 2 is being multiplies by the π.

YOU MUST GIVE 2π A " HOME OF ITS OWN", BECAUSE IT WILL CREATE A LARGE DIFFRENCE AS YOU WILL SEE

pretty color = good for eyes, and when its good you should remember it this way. So here is the equation as it is properly inputted into your calculator.

(-.252680255 ) x (366/(2π)) + 80.5 = 65.7811

ROUNDED OFF IT WOULD BE THE 66TH DAY, THATS OUR FIRST SOLUTION.

SECOND SOLUTION USING ◊ =3.3943

◊= [2π/366(d-80.5)] = 3.9343

(366/2π)[2π/366(d-80.5)] =3.3943(366/2π)

the (366/2π)(2π/366) reduce each other

so we are left with

d-80.5= 3.3943(366/2π)

d= 3.9343(366/2π) + 80.5

plug into calcualtor

d= (3.39427909) x (366/(2π)) + 80.5

d= 278.2188

ROUNDED OFF WOULD BE THE 278TH DAY, THIS IS OUR SECOND AND FINAL SOLUTION

Now all we are left to do is to convert the day into dates.

And this is how our final grpah should look like

To make everything easier to read i will rewrite only the solutions to every question

b) write equations for the function; a sine and cosine equation.

S(d)= -3 sin[2π/366(d-80.5)] + 6.25

S(d) = 3 cos [2π/366(d-(-11))] + 6.25

c) Use your equation to predict the time of sunrise on April 6.


On April 6,we have predicted that the time of sunrise will be at 5:28am.


d) What is the average sunrise time throughout the year?

The average sunrise time throughout the year would be at 6:15am.


e) On what days will the sun rise at 7:00am?

On Mar 7 and Oct 5 the sun will rise at 7:00am

Our next scribe is JessicaJill, who will scribe for Tuesdays class,and im apologizing in advance for any mistakes and anything you cannot understand feel free to correct me, and ill make sure ill make the changes ASAP.