Scribe Scribe Scribe: The Reciprocal Function

Hi, my name is will and I am your scribe for September. 29/06. Before we were about to begin our teacher was congratulating Jess for a well done scribe post that made it into the hall of fame of 2006-2007 which I as well would like to congratulate too. NICE GOING JESS!!!! Soon after that our teacher had to take a call which almost took about 10 minutes. No worries though because we were still able to complete our lesson of today.

Our teacher gave us this on the board:

Write the reciprocal of each number. Reciprocal by meaning of 1/x where x= the number.

a)
Question: 0 1 2 4 10 100 1000 1000000

Answer: Und 1 1/2 1/4 1/10 1/100 1/1000 1/1000000

b)
Question: 0 1 .5 .25 .1 .01 .001 .0000001

Answer: Und 1 2 4 10 100 1000 1000000

Concluding to the first problem a), we see that our numbers from 1 - 1000000 are increasing while the answer to the reciprocal from und - 1/1000000 is decreasing.

The same goes for the second problem b). We start with the answer from number one which is 0 instead of undefined - .0000001 and now we see the reverse situation when our question is decreasing while our answer is increasing.

AND ON BEHALF OF OUR TEACHER SAYING THIS:

"MATHEMATICS IS THE SCIENCE OF PATTERNS" is what we see in this problem.

Before we continued with our lesson our teacher wanted to revise why"0" is undefined when it comes to reciprocating it. Mainly, Reciprocating is the reverse process of multiplication which is division. So say we do this:

Multi. Reverses to: Divi.
2 x 3 = 6 6/3 = 2
3 x 4 = 12 12/4 = 3
4 x 5 = 20 20/5 = 5
5 x 6 = 30 30/6 = 6
6 x 7 = 42 42/7 = 6

Here we see that multiplication is like a forward process to getting an answer. In our division part we see a Reverse process but still both multiplication and division are still using the same values.

When we use the value "0" we get this:


Multi. Reverse to: Divi.

2 x 0 = 0 0/0 = und
3 x 0 = 0 0/0 =
4 x 0 = 0 0/0 =
5 x 0 = 0 0/0 =
6 x 0 = 0 0/0 =

When "0" is evaluated in multiplication, we see that the answer is still "0". When dividing "0" we think that we should get the reverse process of multiplication. But in real mathematics "0" when divided is still "0". Concluding that "0' is always undefined because it cannot be reciprocated.

After doing all this we then started to take the knowledge we gained of reciprocating numbers and plugging it with transformations.

The Reciprocal Function

The basic equation for a reciprocal function is: y = 1/f (x)

Step 1:
To determine our reciprocal function we must start with finding our asymptotic behavior along our x-intercepts/roots. Where y equals zero we draw our vertical dotted/dashline. If the point is at the origin we draw the line at the origin.

Step 2:
We then imagine a horizontal line on the graph in order to find our invariant points which is y = 1 or y = -1.

Step 3:
We then draw our curves. From the invariant point where y = 1 to the Asymptote we can see that our line is decreasing y-values so our reciprocal will be increasing y-values up the y-axis and will never touch the asymptote. If we look at the invariant point y = 1 approaching infinite we draw the reciprocal which will be decreasing y-values and will never touch the x-axis. The same process would be used with y = -1

Note: The asymptotic behavior is a line that can never be touched as the curves increase or decrease.

Step 4 (if y = x²):
If y = x² - 4 then our vertical shift which is -4 will be reciprocated and will be -1/4 if y = x².

Absolute value function
***If an absolute value function was present that has a positive y-value above the x-axis and has a negative y-value below the x-axis, simply flip that exact line/curve as a reflection over the x-axis so that all values have positive y-values.


So first we started with:

f(x) = x to f(x) = 1/f(x). Here we see a table values

y 1/f(x)
1 1
2 .5
3 .3
4 .25
5 .2

and we get this:




This graph is our basic reciprocal function f(x) = 1/f(x). Note that our asymptote is x = 0 because our equations has no x-values affected therefore the vertical line is drawn at y = 0. We then look at our invariant points y = 1. Once that has been determined, we see that from our invariant point to the asymptote, our y-values are decreasing so then we draw our new curve increasing going up the y-axis but will never touch the asymptote. Where we see the invariant point y-increases towards infinite we will reciprocate that and will draw a curve decreasing. The same could be said at y = -1.

Example 1:
f(x) = x+4 to f(x) = 1/x+4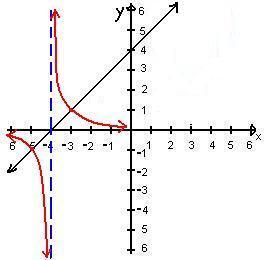




Here we see the same idea except for one thing and that is our asymptote is at x = -4 because our curve intersects at the x-axis at -4 , then we draw our curves.

Example 2:
f(x) = x-2 to f(x) = 1/x-2


This is the same as well but our asymptote is at x = 2, then draw the curves.

Example 3:
f(x) = x²-4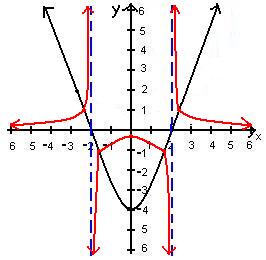


This graph has a parabola which is shifted 4 units down the y-axis and this time we will have roots or x-intercepts at both -2 and 2 because square root of 4 is +/- 2 so we draw our vertical asymptotes. We then draw our curves which are the same if reflected over the y-axis. Finally we have -4 where our parabola starts and will reciprocate to -1/4 so that the two curves coming towards the y-axis of the new graph will intersect at -1/4.

Example 4:



In this graph we draw our vertical asymptote at x = -4 then we draw our curves. Note that the green dot indicates that the original graph does not have an arrow so our reciprocating graph will have a stopper equal to the x-value. The yellow dot indicates that our new graph is decreasing more rapidly because of the original values that have a rapid increase starting at (2,2).

Example 5:
f(x) = |x|




The only difference in this graph is that it is an absolute value function so the negative values of y will be flipped to positive values over the x-axis.


Example 6:
f(x) = |x² - 4|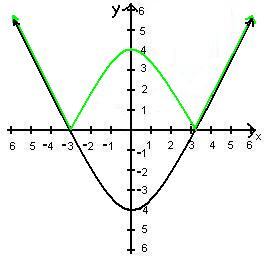


This graph is the same as Example 5, however it's a parabola so all the negative y-values will be reflected over the x-axis in order to make them positive.


So this is our lesson of today... I apologize for any mistakes done on this scribe eg. grammer and this was rushed. This lesson is pretty straight forward and is easy to understand. If you have any questions/concerns or heck just correct me on my mistakes I'd be glad to hear from you... Thx for reading my scribe.....the next scribe is azn_chilly.