Scribe Post - Transformations (James VS The Ferris Wheel)

Hey everyone it's James, it's my turn to be scribe today. To be honest I was not really prepared and spent about an hour playing around with those graphing programs. To let everyone know I will be using the program MGV. Hopefully I will explain everything easy enough for you guys to understand.

Today in class we discussed a problem from the last homework assignment.


Given:

Max Depth : 20 metres @ 8 am
Min Depth : 8 metres, 6.2 hours later

Find:

The Period, Equation(s), Depth @ 10 am, and Time where the water is 10 meters deep.


Ok, so lets start! We all know this is a transformations graph, so let us start by find the values of A, B, C and D. When I talk about A, B, C and D, I mean the values of the equation f(x) = Asin/cosB(x-C)+D.

First of all write down the values A, B, C and D like shown below.

*NOTE* Since we are looking for Equations too, make one for both sin and cos.

Cos	Sin
A=	A=
B=	B=
C=	C=
D=	D=

Now that we have that done, with the given values of 20 and 8 , plot them on a graph along the y-axis like shown below. Be sure to label your y-axis! The y-axis we will now call the "Depth" or "d".


To get the period, we need to find out what point on the graph makes one wave along the x-axis. The x-axis we will call the "Time" or "t". Again do not forget to label the x-axis. With the given depth 20m @ 8am, we must label the time along the x-axis like shown below. Where 20m is the max, 0 on the x-axis will be represented by 8am and where 8m is the min, 6.2 on the x-axis would be represented by 2:12pm. How do you get that you say? Well let me show you!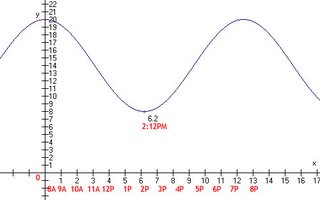


Where 8am is the origin aka 0, 6 hours after 8am would be 2pm. 6.2 hours after 8am would be 2:12pm. To get the minutes, we have to find how many minutes in an hour, which is 60. 1/10th of 60 is 6. So that means .1 hours would be 6 minutes! Get it? I hope so, so lets move on!

*The Period*
Now draw a wave starting from the points that we plotted. As you can see below, the graph looks like a cos graph. It looks like it has given us only half the cos graph, so to get a full graph we must multiply 6.2 by 2. The answer is 12.4 which is our period. To represent the period we must put it in rational form. Since 2π is one period we shall put 2π over 12.4. Now we can start filling in the spaces as shown below.

Cos	Sin
A=	A=
B=2π/12.4	B=2π/12.4
C=	C=
D=	D=

After all that we should have a graph shown like below.


*Equations*
The Equations are easy to find, first of all we will find A.

A: Is the vertical expansion/compression of a graph.
To get A, we must find the sinusoidal axis. The sinusoidal axis is the center between the max and the minimum, in this case it's 14. To get A, all we do is subtract 14 from the max(20). The answer is 6.

B: Is the horizontal stretch of a graph.
We already have B because it's the period

D: Is the vertical shift of a graph.
To find the vertical shift all you need to do is find how far the sinusoidal axis is from the x-axis. In this case it is 14.

C: Is the horizontal shift of a graph.
Last but not least we have the horizontal shift. Since we have two equations(sin and cos) we must find two values. Cos is easy because originally we graphed it, so the value of C for cos is 0. Sin = Cos when C = -3.1. Why -3.1? If you plug it into y=sin(x-C) you will get y=sin(x+3.1) where the sin graph shifts left 3.1 units.

Now we plug all the values in and we get our equations + the final graph shown below.

Cos	Sin
A=6	A=6
B=2π/12.4	B=2π/12.4
C=0	C=-3.1
D=14	D=14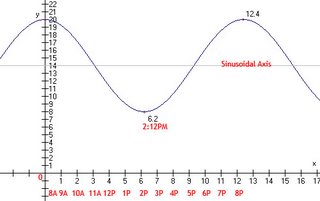

*Depth @ 10 am*
To find the Depth at 10 am, all we need to do is add 2 two 8am. So at point 2 at the x-axis is 10am. Then all you do is plug in the value 2 into "x" in either equations to get your answer. The equation would be y = 6cos[2π/12.4(2)]+14. The answer is 19.999 meters.

*Time water is 10 meters deep*
To find this all you need to do is plug in 10 for "y" and solve. So the equation would be 10 = 6cos[2π/12.4(x)]+14.

Here's the equation to find time.

d(t) = 6cos[2π/12.4(x)]+14
10 = 6cos[2π/12.4(x)]+14

let 2pi/12.4x = Θ

10 = 6cosΘ+14
-4 = 6 cosΘont>
-4/6 = cosΘnt>
-2/3 = cosΘ</font>

Two Solutions
Θ = 2.3005, 3.9827

Therefore the times the water would be 10 meters deep is at 2.3005 and 3.9827.


James Vs. The Ferris Wheel (Coming Soon)

A Ferris Wheel of Radius 25 metres, placed one metre above the ground varies sinusoidally with time the ferris wheel makes 5 revolutions every 2 minutes with james sitting 26 metres above when it starts to rotate upwards.

a) Write 2 sinusoidal functions for James' height above the ground.

b) How high above the ground would James be 16 seconds after the ferris wheel begins turning?

c) How high would a person be 16 seconds after they began the ride?

d) For how many seconds, during each rotation, is a person more than 35m above the ground?



Well I hope everyone understands my scribe post, thanks to Jhoann for helping me with some notes :P.

The next scribe will be! JessicaJill

Happy Scribing!

- James