Scribe Post, Transformations

Alright, so I was the scribe post for Wednesday's class. In our morning class we did our pre-test. Yes, our pre-test. We then worked in groups to agree on what we thought were the right answers, and handed in one paper.

Mr. K started our afternoon class by pointing out how a majority of the class was having trouble with the word problems, judging on our BOB's. So we were given an in-class assignment to work on for 15 minutes as a group and come up with the answers.

Ferris Wheel Function

As you are waiting in line to ride the Ferris wheel at the state fair, you begin to be hypnotized by the repetitive motion of the seats. The seat is at the bottom; it's halfway up; it's at the top; it's halfway down; it's at the bottom; it's halfway up; it's at the top...

You decide to time the wheel, and observe that the ferris wheel makes 4 complete revolutions every minute. You also assume that the diameter of the wheel is 100 feet because a sign beside the wheel says "Climb 100 feet into the sky on our Ferris wheel." However, you note that when you get into a seat, the seat is about 3 feet off the ground, so technically the maximum height a person would reach would be...?

a) Write two equations, one sine and one cosine, that would represent the distance above the ground as a function of time. Let t=0 be when the seat is at the lowest point on the wheel.
b)How high will a person be 10 seconds after they begin riding the ferris wheel?
c) How long after a person gets on the ride will they actually be 100 feet in the air?
d) How long, during each revolution, is a person more than 60 feet in the air?

So, the first thing you should do is, graph the function. Let's get our facts straight. We know that because you're going 100 feet into the air and you'll be 3 feet above the floor, the maximum height you'll reach will be 103 feet. To find what your average value will be, we take our minimum and our maximum, add them together, and then divide our answer by 2. So since 3 is our minimum, and 103 is our maximum, 103 +3 = 106, 106/2 = 53. Since 100 feet is the amount existing between the minimum and the maximum, we can say that the amplitude will be half of 100, which is 50. Lastly, we know that four revolutions takes one minute, so one revolution will take place in 1/4 of a minute, which is 15 seconds. Now we take all this information and graph it, as well as use it to build our equations for question a.

a)

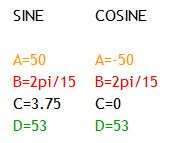
h(t)=50sin[2π/15(t-3.75)]+53
h(t)=-50cos(2π/15t)+53

b)To answer this question, all we need to do is to take either of our equations and substitute t with 10.

h(t)=-50cos[2π/15(10)]+53

Punch it into your calculator and you should get 78 feet.

c) For c, we replace h(t) with 100

100=-50cos(2π/15t)+53

We don't like what's in those brackets because it makes working with it really messy, so we let Θ=(2π/15t).

100=-50cosΘ+53
47=-50cosΘ
47/-50=cos
2.7934=Θ

REMEMBER: You shouldn't round anything off until you get your end result, just store it into your alpha keys. I'm only rounding it off for the sake of having a number represented.
Now we take that answer and plug it into that "monster" of a number.

2π/15t=2.7934
(15/2π)2π/15t=2.7934(15/2π)
t=2.7934(15/2π)
t=6.6688

A person will be 6.67 seconds into the ride when they hit 100 feet in the air.

d) Just remember that these questions are the same thing as the Jho-Ann's bicycle questions. So we substitute in 60 for h(t).

60=-50cos(2π/15t)+53

LET Θ=(2π/15t)

60=-50cosΘ+53
7=-50cosΘ
7/-50=cosΘ
1.7112=Θ

We know that COSINE is negative in quadrants II and III. To get the second solution in quadrant III, we have to subtract Θ from 2π.

2π-1.7112=Θ4.5719=Θ

Now we solve that big monster.

1.7112=(2π/15t)
(15/2π)1.7112=t
4.0853=t

4.5719=2π/15t
(15/2π)4.5719=t
10.9147=t

Now we have to subtract both of the values from each other to get the amount of time the ferris wheel was 60 feet or higher above the ground.

10.9147-4.5719=6.8293

During each revolution, a person is 60 feet or more in the air for 6.8293 seconds.

Then, before class ended, we were given a quick problem to solve on our own.

A low tide of 4.2 m in White Rock, BC occurs at 4:30 AM. The next high tide of 11.8 m occurs at 11:30 AM the same day.

a) Write 2 sinusoidal functions, 1 sine and 1 cosine, then describe the tide flow.
b) What is the tide height at 1:15 PM that same day?

This is what the graph would look like:

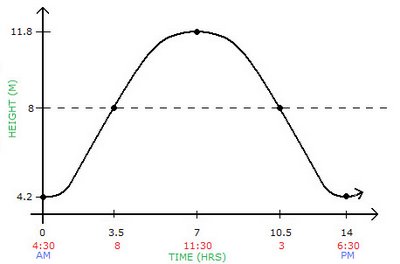
And by using this infomation you can answer question a.

a)
h(t)=3.8sin[2π/14(t-3.5)]+8
h(t)=-3.8cos(2π/14t)+8

The tide flow has an amplitude of 3.8 m, a period of 14 hours and has an average value of 8.

b) For b, we plug in 1:15 into our equation as a value of time, but it has to be converted into the proper number. All we do is we find the difference between 4:30 AM and 1:15 PM.

From 4:30 AM to 12:30 PM, there is a difference of 8 hours, and from 12:30 PM to 1:15 PM, there is a difference of 45 minutes. 45 minutes is 3/4 of an hour, so as a decimal it would be .75, and we can say that 1:15 PM would be 8.75 on our graph.

Now we can take either of our equations.

h(t)=-3.8cos[2π/14(8.75)]+8

When you punch it into your calculator you should get 10.6870 m.

The tide height at 1:15 PM will be 10.687 m that same day.

And that was how we ended our class. Finally! I'm done my scribe. Sorry it took forever to post up.