Scribe Post:Exponents and finding other ways to write a number using exponents

Hi it's Ashley and I'm the scribe for today!
In class Mr.K wrote down 5 numbers on the board and told us to come up with 4 different ways to write down the number using exponents. The numbers were 2, 4, 3, 1/2 and 4/9. Seems hard huh? But don't worry once you see the pattern it gets easier.
By the way for those that don't know, this symbol ^ means to the power of. So for example 2^4 means 2 to the power of 4 which equals 16.

*Remember that there infinite ways to find another way to write a number.*

Then Mr.K said that knowing how to do that you can do this. I'm pretty sure that's what he said.
2^x=32 (well remember 32 can be written as 2^5)
2^x= 2^5
x=5

3^x-1 = 27 (find a way using the number to find the same base, in the case 27 can be written as 3^3)
x-1 = 3
x=4

In these questions like the questions above you are asked to prove and find the value of x. The key to these questions is that the idea is to find another way to write the number using a useful base. What you want is to look for a common base for both expressions. The reason why you look for a common base is because if the bases are the same then the exponents must equal the same. Then you just solve for x. It will be further understood when you see the questions below since I'm poor at explaining -_- Oh but the questions might look a little weird since it's hard to write exponents on the computer so here's an example of how it looks like on paper:

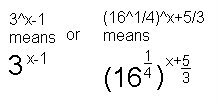
1) 2^3-2x = 1/4^x-3/2
the next step is to find another way to write the number using a useful base. in this case we want the base 1/4 to be 2.
2^3-2x = (2^-1/2)^x-3/2 (1/4 equals 2^-1/2)
2^3-2x = 2^(-x/2+3/4) (what you do here is multiply -1/2 to x-3/2 which gives you -x/2+3/4)
now that you have the same base for both expressions you can now solve for x.
3-2x = -x/2+3/4
4(3-2x) = (-x/2+3/4)4 (you want to get rid of the denominator which is 4 so you multipy both sides by 4)
12-8x = -2x+3
12-3 = -2+8
9 = 6x
3/2 = x

2) 3^4x-1 = 27^2x

Like in the previous question you want to find another way to write the number so it can have a common base
3^4x-1 = (3^3)^2x (27 equals 3^3)
3^4x-1 = 3^6x
now sove for x
4x-1 = 6x
-1 = 2x
-1/2 = x

The question below is a little bit trickier if you don't know the laws of exponents. So remember that if you multiply powers with the same base then you add. If you divide powers with the same base then you subtract.
3) (3^x)(27) = 81^2x+1
now look for another way to write the numbers using a useful base. for this question a useful base would be 3 since both 27 and 81 are multiples of 3.
(3^x)(3^3) = (3^4)^2x+1 (27 equals 3^3 and 81 equals 3^4)
*now remember when you multiply powers with the same base you add
3^x+3 = 3^8x+4 (3^x*3^3 the power x and 3 are added together so they become x+3)
solve for x:
x+3 = 8x+4
3-4 = 8x-x
-1 = 7x
-1/7 = x

And just when I thought class was over Mr.K had to put up two more questions on the board. Gheez....

4^2x-4 = 1
like in previous questions rewrite the base so that both numbers have the same base. at first some would think of changing the base 4 into base 1 by having the power be 0 but then the 0 would cancel the whole exponent. so instead you should do this:
4^2x-4 = 4^0 (the 4^0 would equal 1 since any number to the power of 0 expect 0 itself equals 1)
then you go on from there solving x
2x-4 = 0

2x = 4
x = 4/2
x = 2

For this question at first it looks hard but actually what you do is balance the equation first so you can get the power by itself like this:
5^(2x-1)+2 = 3
5^(2x-1) = 3-2
5^(2x-1) = 1
next step is similar to the previous question in that you re-write the 1 to be the same base as 5 by having the power be 0.
5^(2x-1) = 5^0
2x-1 = 0
2x = 1
x = 1/2

So this is the end of my post and if there are any mistakes just comment. Also if it's hard to read sorry about that but for some reason my spacings didn't turn out right. I wonder why it does that? By the way the homework is Ex.20. Apparently if you understand what we did in class the homework will be super easy but remember we still have the test on Trigonometric Identities tomorrow guys so study hard!! Mr. K said the last page of the test will have the identities on it so that's a relief. Good luck everybody!

the next scribe will be Jason!