Scribe post: Transformations

Hello guys! I'm Daphne and I'm the scribe for today. On our second period pre-calculus, we did some exercises about transformation. First, Mr. K gave us an equation needed to be solved by sketching a graph. Second, he gave us word problems that must be equated. Lastly, he gave us an equation that must be answered by a process on which of the following operation must be done first. Here are the questions we solved in the class.
A) Sketch the graph:

f(x)= 1/x²-1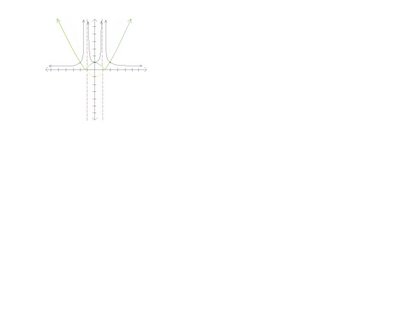






















Steps in the making the graph of f(x) = 1/x²-1
1. Draw the original function x²-1
2. Draw the absolute function. Move your negative y values to the positive y values.
3. Look for roots/ zeros/ x-intercept and draw your asymptotes.
4. Look on the graph for -1 and 1 and draw the anchors.
5. When the points are plotted, all the arrows that have decreasing numbers will be changed to increasing values and all the arrows that have increasing numbers will be changed to decreasing values.


B) y= f(x)

Write the formula for each set of transforamtions done to y

1. translate 2 units right
Answer: y= f(x-2)
2. Compress the graph horizontally by a factor of 5
Answer: y=f(5x)
3. Stretch the graph horizontally by a factor of 2 and translate 3 units down.
Answer: f((1/2)x)-3
4. Reflect the graph in the y-axis and strecth it vertically by a factor of 3
Answer: y= 3f(-x)


C) y= f(2x-4)+1

Make the procedure on this equation and identify which operation will go first in graphing this.

1. Stretch the graph vertically by factors of 3
2. Compress the graph horizontally by factors of 2
3. Translate it 4 units to the right
4. Translate it one unit up

After answering a couple of questions, Mr. K told us to compare our answers with our adjacent classmate. We were given 60 seconds to do that. As a result, we came up with the answers written above. Then, we were asked to put out our math dictionaries because a new lesson will be added but before that Mr. K gave us a phrase to remember.

"Stretches first before translations"

MATH DICTIONARY

EVEN FUNCTIONS

Graphically: A function is "even" if its graph is symmetrical about the origin.

The function are eve

These are not

Symbolically (Algebraically): a function is "even" IFF (if and only if)

f(-x)= f(x)

Examples: Are these functions even?

1. f(x)= x²
f(-x)=(-x)²
= x²
since f(-x)=f(x)
f is an even function

2. g(x)= x² + 2x
g(-x)= (-x)² + 2(-x)
= x² - 2x
since g(-x) is not equal to g(x)
g is not an even fucntion



ODD FUNCTIONS

Graphically: A function is "odd" if its graph is symmetrical about the origin.

These functions are odd (if its graph)

These are notSymbolically (Algebraically): A function is odd IFF (if and only if)

f(-x)= -f(x)

Examples:

1. f(x)= x³- x
f(-x)= (-x)³- (-x)
= -x³+ x

since f(-x)= -f(x)
f is an odd function

2. g(x)= x³- x²
g(-x)= (-x)³ - (-x)²
= -x³ - x²
-g(x)= (x³-x²)
= -x³+ x²
since g(-x) is not equal to -g(x)
g is not an odd function

Sketching the reciprocal function graphs y= 1/ f(x)

IMPORTANT: 1/ f(x) is not equal to f^-1 (x)

i.e a reciprocal is not the same things as an inverse

Example:

Sketch the graph f(x) = 1/ x²-4

THE RECIPROCAL TRIGONONMETRY FUNCTIONS


f(x) = cscx

f(x)= 1/ sinx

f(x)= secx

f(x)= 1/cosx

f(x)= cotx

f(x)= 1/tanx

Sketching f(x)

STEP 1 Sketch f(x)

STEP 2 Reflect the postion of the graph of f(x) that is below the x-axis above the x-axis.

Example:

Sketch f(x)= x²-4

After writing everything in our Math Dictionary, Mr. K discussed an unfinished discussion about the different seasons in the earth affected by its slanting axis. Well then guys, this is my scribe post and I hope you enjoy viewing my page!!!!!