SCRIBE # 1 !?, intro to circular functions

GREATINGS!! FELLOW STUDENTS! Jefferson is the scribe for today.
Mr K started us off with a one billion dollar question, why does a circle have 360 degrees? Well one classmate said that in ancient times back when there were Babylonians, they had numbers with a base of 60. We count numbers with a base of 10 mind you. Their calendar had 360 days in a year, and one full cycle (sun orbiting around our planet) would take 360 days. Mr K agreed, however he said that there was another reason for why a circle had 360 degrees. He then asked if we could use a different number instead of 360. Christine said 100 because it was easier to use. Mr K said that the British liked Christine’s idea so much, that they actually used it. Instead of degrees, the British called it; “gradians” .There was actually 400 gradians in a circle instead of 100 gradians. Mr K then asked us a really tough question. Why is 360 degrees in a circle? Wooo, what a toughie. Mr K asked us what the factors of 360 are. We then regurgitated , “ 1,2,3,4,5,6,8,9,10,12,15,18,20,24,30,36,40,45,72,90,120,180,360. Mr K then asked, “What are the factors of 400? “ We the regurgitated, “1, 2, 3, 5, 8, 10...etc” Mr K said that 360 is evenly cut up using more number(factors) than 400 (which lead to the fall of gradians, you said it folks, gradians didn’t catch on)
Now acting like a magician, Mr K asked for a volunteer. What trick does Mr. K have up his sleeve? Let’s find out shall we? Jessica volunteered to be the guinea pig- volunteer. MR told Jessica to spread her fingers as far apart as possible and place her thumb and pinkie onto a circle/graph that Mr. k drew during his lecture. Jessica gets her own measurement from the space from her thumb to pinkie called “Jessica” units. He then took a towel and placed it from the center of the circle to the circumference. He explained that the towel represented the radius of the circle. He then rapped the towel around the half of the circle. He said that the measurement was indeed NOT Jessicas, but RADIANS. The number of towels that took to be wrapped around half of a circle was 3 and a bit. That total length is none other than PI!!! And I’m not talking about the desert. A rough definition for pi is a measurement was formed from wrapping the radius around half a circle 3.14 times. And again Mr K asked us another hard to find answer. “Why are there 2 triangles in a geometry set” half of us never even thought about it. Well. The first triangle, the isosceles (triangle that has sides of the same length)/ right triangle, has 45 degrees in it. And the other triangle had a 30 and 60 degrees in it. 30,45 and 60degrees are the angle measurements that are used the most. On the unit circle 30 degrees are broken into sixths, 45 degrees into quarters, and 60 degrees in to thirds.




the red numbers (45 degrees and so on) brake up the unit circle into quarters

the green numbers ( 30 degrees and so on) brake up the unit circle into sixth

the blue numbers (60 degrees and so on) brake up the unit circle into thirds

here's the unit circle in radians

Now where did those triangles(from our geometry set) come from? It pretty much came from the unit circle. 45 degrees is pi/4.

How do we convert degrees into radians you ask? Well its simple, follow this guideline : 180º/Π = D / Θ. This translates to : 180 degrees is to pi the same way to an angle is to radians.

Mr k then gave us a practise problem to do:

What is 40 degrees in radians?
*remember to follow the guideline

180º/Π = D / Θ
180º/Π = 40 º/ Θ
180Θ = 40Π
Θ = 40Π/180
Θ = 2Π/9

Here’s another one:

What is 50 º in radians?

180º/Π = D / Θ
180º/Π = 50/ Θ
180Θ = 50Π
Θ = 50Π/180
Theta = 5Π /18

What is 2 radians in degrees?
180º/Π = Π /2
360/Π = (ΠΘ)/Π
114.592 º = Θ

And thus ends our scribe post- NO WAIT THAT WAS ONLY THE FIRST CLASS, WE HAD TO CLASSES TODAY!!

In our second class, Mr. K attacked(don’t mean literally) us with math problems on the white board. >

Convert to radians

A) 25 º

b) 260 º

A)
180 º / Π= 25 º/ Θ
25Π/180 = Θ
5Π/36 = Θ

b)
180 º / Π = 260 º / Θ
260Π/180 = Θ
13Π/9 = Θ

Convert to degrees

A) 4.5

b) 12Π/5

A)
180 º/ Π = Θ / 4.5
810/Π = Θ
257.831 º = Θ

B)
180/Π = Θ/ (2Π/5)
2160Π/5 = Π(Θ)
432 = Θ

Find the indicated angles:

a)

A = 75 º since angle a is opposite of 75 ºthen angle a = 75 ºbecause they are both opposite angles

b)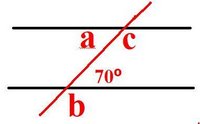

A = 70 *angle a and 70 º are both alternate angles so the equal
C = 180 - a
C = 180 - 70
C = 110
B = 180 - 70
B = 110

* angle b is congruent with 70 degrees

c) find the complement of 50 degrees

90º- 50º = 40 º

*compliment is and angle whose sum adds up to 90 º

d) find the complement of pi./ 3

Π/2 - Π/3 = 3Π/6 - 2Π/6

Π/2 - Π/3 = Π/6

*”complement is and angle whose sum adds up to 90 degrees” 90 degrees in radians is pi/2

E)find the supplement of 15 º

180 - 15 = 165

* supplement is an angle whose sum adds up to 180 º

F) find the supplement of Π/4

Pi=Π/4 = 4Π/4 - Π/4
Pi - Π/4 = 3Π/4

Mr K then gave us a brief explanation about the right triangle and the Pythagorean theorem
Pythagoras was a Greek man who was famed for being very intelligent, unfortunately he was super ugly according to Mr. K
He drew 3 different sized right triangles and asked us how they are the same?
He then referred to something that we’ve learnt back in grade 9: soh cah toa. Which means sin = opp/hyp, cos = adj/hyp, and tan = opp/adj.
He then made us take out our calculators and challenged us to a race. Mr k will give us an angle to input into our calculator sine of 50. Well out 4 questions, it seemed that Mr. k had the upper hand even though he used his head to calculate the answers instead of using a calculator. The answers where all the same too : .5 and -.5 where the answers to the questions
He said that all the right triangles ended up with the same answer because they are virtually the same but in different sizes. He can shrink on down as small as possible and come up with an answer that is 0.5 and blow another triangle up and it would still be the same answer.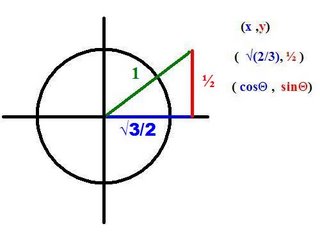

you may wonder what this triangle thing means. if you compress triangle as small as possible the hyp. will have a value of no less than 1 as you can see. with a bit of work from the pythagorean theorem i got the other 2 numbers. now on a graph we would express ordered pairs in terms of x and why, but on a unit circle it's express differently. its expressed in terms of sin and cos. x is cos, y is sin.

thats all for today, Jefferson SIGNING OFF!

oh yes

vgamecom!!you're scribe, good luck!and have fun!

:)=3