3rd Scribe Post

Hey people! I’m Jessicca, and I’m the scribe. Today we made our first entry into our Math Dictionaries. A lot of information was added to our dictionary, so here it is:

Circular Functions:

Degree: A unit of measure for angles; there are 360 degrees (360˚) in a circle.

Radian: A unit of measurement for angles; there are 2π radians in a circle. A “radian is an angle measurement without units.


Converting Degrees and Radians

A / 360˚ = R / 2π

or

A / 180˚ = R / π

A – is the given angle in degrees
R – is the given angle in radians

Examples: 1. Find 20˚ in radians.

20˚ / 360˚ = Θ / 2π
40π = 360Θ
40π / 360 = 360Θ / 360
Π / 4 = Θ

1. Find π / 5 radians in degrees

Θ / 180˚ = (π /5) / 2π
2 π Θ = (180) (π / 5) à reduce (180) (π / 5) = 36π
2 π Θ = 36π
2 π Θ / 2 π = 36π / 2 π
Θ = 18˚

Complimentary angles: 2 angles whose sum is 90˚ or π / 2.

Supplementary angles: 2 angles whose sum is 180˚ or π.

(Vertically) Opposite angles: angles opposite each other of the intersections of two straight lines are congruent.

Examples:

mnemonic : X

Transversal: A straight line that intersects two or more parallel lines.

Example:

Alternate angles: two interior angles, on opposites sides of a transversal are congruent.

Example: Corresponding angles: two (or more) angles on corresponding sides of a transversal are congruent.

Example:

Arc Length:

For radians:

R / 2π = L / 2πr

R is an angle in radians
L is an arc length
r is the radius

D / 360˚ = L / 2πr

D is an angle in degrees
L is an arc length
r is the radius

*an arc length is part of the circumference of a circle.

Examples:

1. A circle with radius 10 cm has a central angle of 60˚. What arc length is subtended by that angle?

Solution:
60˚ / 360˚ = L / 2π(10)
(60)(20π) = 360 L
1200π = 360 L
10.742 cm = L

2. A circle with radius 10 cm has a central angle 2π/9. What arc length is subtended by the angle?

Solution:
(2π/9) / 2π = L / 2π(10)
(2π/9)(1/2π) = L / 2π(10)
1 / 9 = L / 2π(10)
20π = 9L
6.981 = L

Standard Position: an angle is in “standard position” if its initial arm begins at the origin and lies along the positive x-axis.

Example:

Θ is standard position
Ø is not is standard position

Coterminal angles: two angles in standard position that share the same terminal arm.

Example:

Θ and Ø are coterminal angles

Sector: A part of a circle bounded by a central angle and an arc length.

Example:

Area of a sector:
In degrees

Θ / 360˚ = A / πr2

Θ / 2π = A / πr2

Θ is an angle in degrees or radians
A is the area of a sector
R is the radius of a circle

Example: A circle has a radius of 10 cm. Find the area of a sector with a central angle of 30˚.

30˚ / 360˚ = A / π(10)2
30(100π) = 360A
3000 π / 360 = 360A / 360
26.180 cm2 = A

The last thing we put in our dictionaries was the Unit Circle: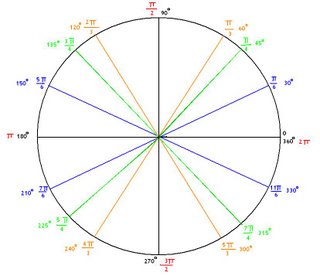

In our afternoon class, we did some problems:

1. Find the arc length subtended by an angle of 130 in a circle with radius 15 cm.

Solution:

130˚ / 360˚ = L / 2 π (15)
360L = 130(2 π (15))
360L = 12 252.211
360L / 360 = 12 252.211 / 360
L = 34.034 cm

Find the radius of a circle if an arc of 3 cm subtended by an angle of π/6.

(π/6) / 2π = 3/2πr
(π/6)(2πr) = 6π >>> (π/6)(2πr) reduces to (π/3)( πr)
(3/ π2) ((π2)r)/ 3 = 6 π (3/ π2)
18/ π = r Or
5.730 = r

3. What is the smallest positive alternate angle of:
a) 2000˚

What Mr.K showed us for this question was to divide 2000 degrees by 360, which gave an answer of 5.55…
Next we subtracted 5, so the percentage .55…. would remain.
We multiplied it by 360 >> 200

Mr. K explained that when you divided 2000 degrees by 360 it would show the number of times 2000 degrees wrapped around the circle. 200 degrees was how much needed left.


b) -5100˚
This question was different. You still did the same procedure, and ended as a result of -60 degrees. But that was not the right answer. A student came up to the board then, and explained to the class what the real answer was, which would be 300 degrees because you’re looking for the positive angle and the negative answer would be wrong.

That's all for my Scribe Post. Thanks for reading!!

The next Scribe is ...... tennyson!