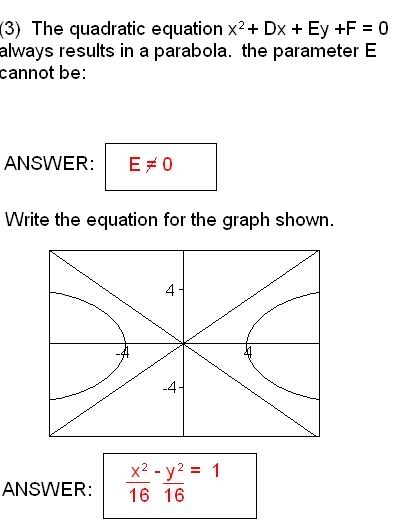
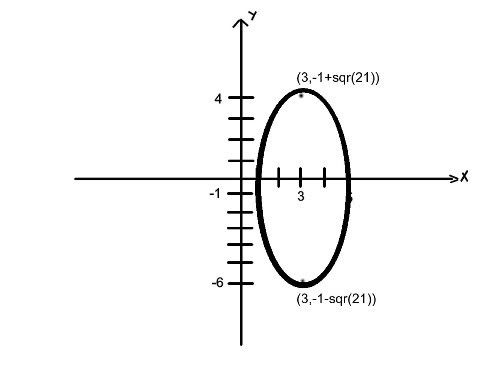
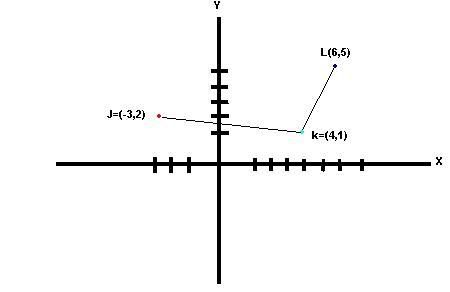
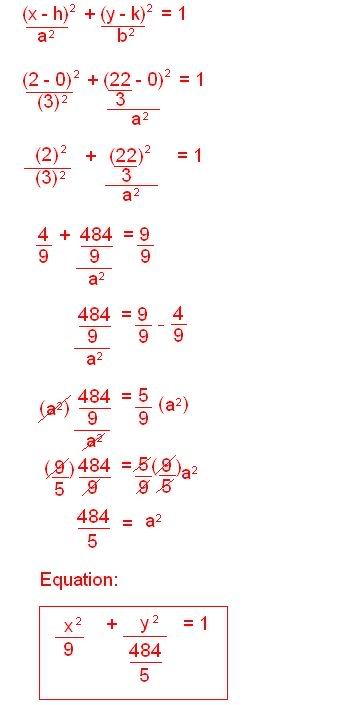the 3rd scribe post of ruschev
PROBABILITY
note:
- Mutually Exclusive : unable to be both true at the same time ; one event taking place prevents the other event from taking place ex) flipping a coin is a mutually exclusive since it can not be heads at the same time.
- drawing a tree diagram will help allot when solving probability questions
- drawing a Venn diagram will also help
- adding probability. P(a)+(b) when the question is an "or" question. ex) 2 boys are running what is the probability of one of these boys win if one boy has 1/4 of winning and one has 2/3 of winning.
-multiplying probability. P(a)*(b) when the event is independent. ex) a boy flips a coin and gets a heads, he flip it again and get a tails. independent does not change the outcome of the next occurring event.
- (~) is the symbol for "not"
- "1" is the highest possible value you can get ; a 100% chance ; more than 1 will result in an incorrect answer ; when you add up all of your probability the numbers you should only get is equal to or less than 1 or zero.
- changing percent into a decimal will make calculation easier
- fraction is our Friend!
Questions:
1. man of war and secretarial are in a horse race, man of war has a 2/5 chance of winning and secretarial has a 1/3 chance of winning..
a) are these events mutually exclusive?
b) what is the probability that one of these horses wins the race?
c) what is the probability that both win?
answers:
a) no
b) probability of man of war winning is 2/5 ; probability of secretarial winning is 1/3 so...
(2/5) + (1/3) = (11/15)
c) (2/5) x (1/3) = (2/15)
Questions:
10 grade 12....40% of the students take math, 35% take history and 15% take both. If a student is randomly chosen. what is the probability that the student takes..
a) math but not history?
b) neither math or history?
Answers:
a) change percent into decimal. P(math) = .40 P(history) = .35 P(~m)= .60 P(~h) = .65
P(M x ~H)= P(.40 x .65) = .26

b)

"green" = students taking math ( 40%-15% = 25% or .25) "brown" = students taking history (35%-15% = 20% or .20) "blue" = students taking both subjects ( 15% or .15) *add up all of our values ( .20+.15+.25 = .60) meaning that there are .40 students that are not taking neither subjects (1-.60 = .40)
Question:
you are dealt a 5 card poker hand, what is the probability that you have "at least one" heart?
Answer:
52 cards in a standard deck of cards and there are 13 hearts * 1 - none leaves all the possibility of "at least one"* *1- none leaves all the possibility of "at least one"* * 1 subtract none leaves all the possibility of "at least one"* * 1 take away all the cards that are not hearts will leave all the cards that are hearts*
39C5 = 39 ( the number of cards that are not hearts) 5 ( 5 card poker hand)
52C5 = 52 (total number of cards) 5 ( 5 card poker hand)
1- 39C5/52C5 = .77
numerator: 39C5 <- 39 cards that are not hearts choosing 5 random cards
denominator: 52C5 <- total cards choosing 5 random cards
"1" <- the highest possible value that you can get ; 100%