Scribe Post
The morning started out with the usual problems nothing new about that.
1) Find the center and radius of the circle: 4x2-12x+4y2-30 = 0
4[(x2-3x+(3/2)2-(3/2)2)]+4y2 = 30
4[(x-3/2) 2-9/4]+4y2 = 30
4(x-3/2) 2-9+4y2 = 30
4(x-3/2) 2+4y2 = 39
4[(x-3/2) 2+y2 = 39
(x-3/2) 2+y2 = 39/4
The center is at (3/2,0) while the radius is the sqr. root of 39 over 2
For what value of k will the circle x2+y2-2x+4y+k = 0 have a radius of 4?
(x2-2x)+(y2+4y) = -k
(x2-2x+1)+(y2+4y+4) = -k+1+4
(x-1) 2+(y+2) 2 = -k+5
Since we want a radius of 4 we add it in
42 = -k+5
16 = -k+5
k = -11
Find the equations of the ellipse with center (3,-1), major axis of length 10 and parallel to the y-axis, minor axis is 4 units long.
(x-h) 2 + (y-k) 2 = 1
b2 a2
(x-3) 2 + (y+1) 2 = 1
4 25
Foci:
C2 = A2-B2
=52-22
=25-4
=21
C =sqr(21)
The foci is measured from the center of the ellipse moving up and down hanging in between sqr(16) and sqr(25) since sqr(21) is the next perfect square above sqr(16) and below sqr(25).
The second half of the class was us working on the hyperbolas that we drew last week, the changes I'm afraid you'll have to ask people in class about since the new additions wouldbe a little confusing for me to show on computer.
Next scribe is JessicaJill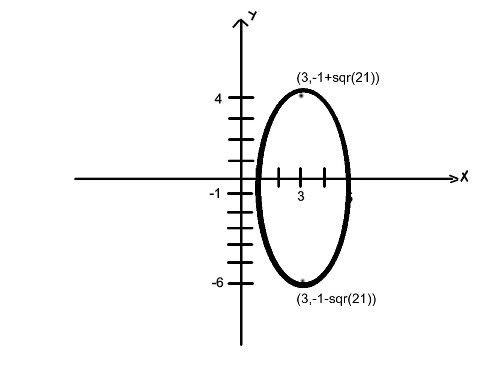

No comments:
Post a Comment