Conics: The Parabola, Circle and Ellipse (Cheek's 3rd Scribe post)

Hello its cheeks again working on today's scribe post on Conics: The Parabola, Circle and Ellipse. We started off by talking about our website reaching its max on 300 mb due the cause of all the images we posted up. So for now on we will be using photobucket to upload our images into our blog. We then watched some videos that were quite hilarious based and mathematics in relation with the real world. Our final video was about a tire then went loose as the driver was driving and how it rolled, flyed, bumped into other cars and reaching its final destination back into the drivers car again and the probability of that was 0.0000001%. Think its possible? Comment it. Our teacher then wanted all of us to comment about how mathematics is used in our other subjects. Think it is? Comment that too.

We continued our lesson where we left off from the anatomy of the parabola...

Our lesson began and ended with our dictionaries:

Deriving the standard form for the equation of a parabola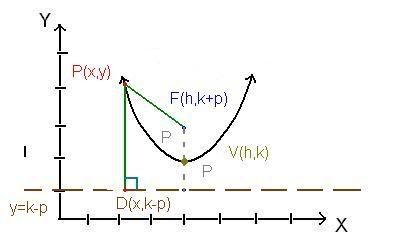

__ __
PF=PD (by def'n)
√[(x-h)²+[y-(k+p)]]² = √[(x-x)²+[y-(k-p)]]² (Distance formula)
(x-h)²+[y-k-p][y-k-p] = [y-k+p][y-k+p] (Square both and simplify)
(x-h)²+y²-ky-py-ky+k²+kp-py+kp+p² = y²-ky+py-ky+k²-kp+py-kp+p² (expan)
if we were to bring the terms that cancel from the left to the right side we simplify to:
(x-h)² = 4py - 4pk (balance)
(x-h)² = 4p(y-k) (factored)
***Standard form for equation of a vertical formula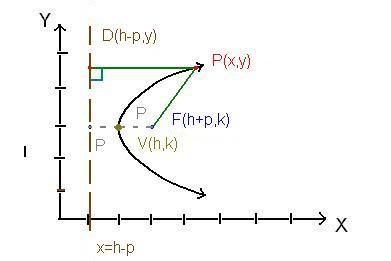


__ __
PF=PD (by def'n)
√[[x-(h+p)]²+(y-k)²] = √[[x-(h-p)]²+(y-k)²] (Distance formula)
[x-h-p][x-h-p] +(y-k)² = [x-h+p][x-h+p] (Square both and simplify)
(y-k)²+x²-hx-px-hx+h²+hp-px+hp+p² = x²-hx+xp-xh+h²-hp+px-ph+p² (expan)
if we were to bring the terms that cancel from the left to the right side we simplify to:
(y-k)² = 4px - 4ph (balance)
(y-k)² = 4p(x-h) (factored)
***Standard form for equation of a horizontal formula
__________________________________________________________

Circle: A locus of points that move such that they are a fixed distance (radius) from a fixed point (centre).

Deriving the standard form for the equation of a circle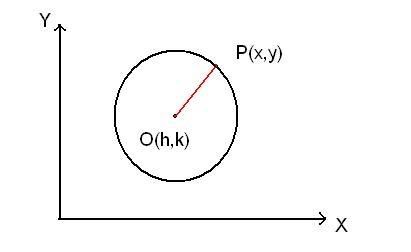


__
OP = r (by def'n)
√[(x-h)²+(y-k)²] = r (Distance formula)
(x-h)²+(y-k)² = r² (standard form for a circle)

__________________________________________

Ellipse: A locus of points that move such that the sum of the distances (focal radii) from fixed points (foci) is constant.


The anatomy of the ellipse

A₁ and A₂ are the vertices of the ellipse
A₁A₂ is the major axis of the ellipse. It is a line of symmetry and its length is 2a
B₁B_{2 are the endpoints of the minor axis.}
B₁B_{2 is the minor axis of ellipse. It is a line of symmetry and its length is 2b.
F1 and F2 are teh foci of the ellipse each focus is C units from the centre.
PF1 and PF2 are called the focus radii. Their sum is always 2a, the length of the major axis.}

The standard form for the equation of an ellipse

Standard form for a horizontal equation

Standard form for a vertical equation



The focal radii property

Suppose P is at A
PF₁ + PF₂ = A₁F₁ + A₁F₂ (by def'n)
PF₁ + PF₂ = A₂F₂ + A₁F₂ (by symmetry
PF₁ + PF₂ = A₁ A₂
PF₁ + PF₂ = 2a

The Pythagorean property

Suppose P is at B
PF₁ + PF₂ = B₁F₁ + B₁F₂
By symmetry we know that
B₁F₂ = B₁F₁
there fore...
PF₁ + PF₂ = B₁F₁ + B₁F₁
PF₁ + PF₂ = 2B₁F₁
By the focal radii property
PF₁ + PF₂ = 2a
therefore..
2a = 2B₁F₁
a = B₁F₁
and by Pythagorean theorm
b² + c² = a² or c² = a² - b²

Thats all for tonight the next scribe is Jefferson