All about Patterns

Hey it's Ashley and I'm the scribe for today and yes I know i didn't do it right away but for those who missed you should have really been there. It was a pretty interesting class because the class was all about PATTERNS and mr.k telling us about how God built the universe and blowing our minds (not literally of course...)

To start off Mr.k posted up the questions that he previously posted the day before on the board.

Expand and Simplify

(a+b)^0
(a+b)^1
(a+b)^2
(a+b)^3
(a+b)^4

To answer this question it's simple just expand and simplify

(a+b)^0 = 1 (because its exponent is 0)
(a+b)^1 = a+b (because its exponent is 1)
(a+b)^2 = (a+b)(a+b) => a^2 + 2ab + b^2

now be smart about the next question
instead of doing this (a+b)(a+b)(a+b) just multiply a^2 + 2ab + b^2 by (a+b) since it will be easier since a^2 + 2ab + b^2 is the same as (a+b)(a+b) and you are just multiplying one more (a+b) since its to the power of 3.
(a+b)^3 = a^2 + 2ab + b^2 * (a+b)
now distribute the a


= a^3 + 2a^2b + ab^2

then distribute the b

= a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3

then gather the like terms
= a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3
= a^3 + 3a^2b + 3ab^2 + b^3

Now do the same for (a+b)^4. Distribute and gather the like terms.
*Do not foil because foiling only works with binomials*

(a+b)^4 = (a^3 + 3a^2b + 3ab^2 + b^3) * (a+b)

Distribute a
= a^4 + 3a^3b + 3a^2b^2 + ab^3

Then Distribute b
= a^4 + 3a^3b + 3a^2b^2 + ab^3 +a^3b + 3a^2b^2 + 3ab^3 + b^4

Gather the like terms
= a^4 + 3a^3b + 3a^2b^2 + ab^3 +a^3b + 3a^2b^2 + 3ab^3 + b^4
= a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4

The other question posted on the board
Look for a pattern

Write the next two rows

1
1 1
1 2 1
1 3 3 1

1 4 6 4 1

Now looking at this question having down the previous question a few of us realized the pattern

The first pattern:

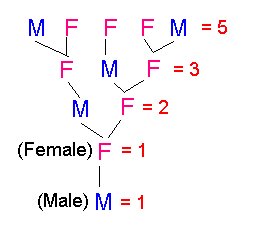
Adding the numbers like this (sorry it's hard for me to explain so a diagram will hopefully help):

The Second Pattern:

The numbers in the triangle are the coefficients to the expand and simplify question.

The Third Pattern:

The exponents on the variable are: a descending and b ascending.
example:

The last question posted on the board:

Evaluate each term (you can use your calculator):

OCO

1CO 1C1

2CO 2C1 2C2

3CO 3C1 3C2 3C3

4CO 4C1 4C2 4C3 4C4

Now if you did this on your calculator you would get

OCO = 1
1 = 1CO 1C1 = 1
1 = 2CO 2C1 = 2 2C2 = 1
1 = 3CO 3C1 = 3 3C2 = 3 3C3 = 1
1 = 4CO 4C1 = 4 4C2 = 6 4C3 = 4 4C4 = 4

In other words.....

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

It's the same as the second question. Neat huh?!

It's interesting as to how all of the three questions written on the board are all related to each other somehow. So how is the last question connected to the first question? Well.... it's better if i show an example:

Then just when I thought there couldn't be more to talk about Mr. K handed us a worksheet which I'll post tomorrow. But it basically showed Pascal's Triangle which is this and I forgot what Mr.k said about pascal so ask him if you want to know who he is.

Now at the bottom of the worksheet it asked if you can find powers of 2, powers of 11 etc....

To find the powers of 2 in the triangle you just add the numbers in each row.

To find the powers of 11 in the triangle just look at it.

Sierpinski triangle is a fractal and well...... a guy named Sierpinski decided to punch out triangles in an equilateral triangle where the area is fixed but the perimeter is infinite. I think that's what Mr.k said but here's what Sierpinski did. He used an equilateral triangle and punched out other equilateral triangles inside it like this: (sorry bad explanation)

Then Mr.K told us to shade in the odd numbers on the triangle which felt like I was back in elementary. We should color more often!

Looks like the Sierpinski triangle doesn't it? If you continued on shading the odd numbers it would be even more clearer. Cool right?!

Next was on the talk about the Fibonacci numbers 1, 1, 2, 3, 5, 8,....

Fibonacci numbers work by adding the last two previous numbers.

1+ 0 = 1, 1+1 = 2, 1+2 = 3, 2+3 = 5, 3+5 = 8

Apparently bees, yes bees follow the fibinacci sequence because a male has one parent which is it's mother and a female has two parents, both a mother and a father.

What else was mentioned in class? Ah yes flowers also respect the fibonacci sequence. You won't find a flower with 6 petals but you will find a flower petal with 5 petals but you won't find a flower petal with 7 petals but you will find a flower with 8 petals, so that's why it's rare to find a four leaf clover.

And Lastly Mr.K mentioned a number which i forgot what the number is called but it has to do with something about dividing your body into parts and it always equals to that number. Sorry but i forgot what he said but it sounded cool. However I'm still not sure as to what part of the lesson was on God building the universe? Oh well....

The next scribe will be.........LISA!!!

and sorry about the picture not showing. i wonder why that is?