ScubaSteve's Third Scribe Post

This just in! Mr.K recently informed that the Flickr assignment has been extended! Memo hurrahs around. So for those who are thinking about flying under the radar, get camera happy! Plus, the favorite number picture will still be allowed for uploading. Aside from the pc40sf06 tag, the favorite number should also be tagged with a 'interesting' and the recent trig assignment be tagged with a 'trigonometry' tag =). Enjoy.

This is ScubaSteve reporting for the third time. I know so far i've topped my post with the previous one, and hopefully you guys are not expecting me to top this one ;_;. The last one was a big one, so many pictures almost jepordized my scribe post (it was spacing out around the end, good thing i finished before it dragged on). Now, today was a double class. We were introduced to Conic Sections, a new unit that i seemed to be already confused about. Its not that i dont understand it, its just tough to re-write in my own words or explain it, so bare with me ^.^; I promise if i scribe again, i'll make up for this post if this is unsatisfactory ;]. Without further adieu, read on my cyber-math classmates.

The first class was an introduction. We learned how to find the eq'n by looking at the graph. Lets look at a basic one first.

Given what is drawn here the formula to find an eq'n of a graph is: (PF=PD) (root->),(x-h)^2+[y-(k-p)]^2 = ,(x-x)^2+[y-(k-p)]^2. First we properly expand the monster that is [y-(k-p)]^2 which ends up being:

(y-k-p)(y-k-p) => y^2-yp-yk+k^2+kp-yp+kp+p2 => y2-2yk-2yp+2kp+k^2+p^2 (its ugly i know but we'll have to bare with it) So putting it back into the original eq'n we'll have...

(x-h)^2+y^2+k^2+p^2-2yk-2yp+2kp=y^2+k^2+p^2-2yk-2yp+2kp => (x-h)^2=4yp-4kp => (x-h)^2=4p(y-k)

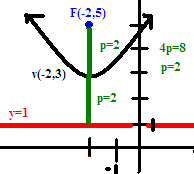
This graphs eq'n is (x+2)^2 = 8(y-3)

Could you recognize simularities in the eq'n that is familiarly applied to the graph? Vertex?

The p is the distance between the Focus (F) to the vertex. It is equal to the distance between the vertex and the Directrix (D)

P can be found by 4p=(coefficient), in this case it's 8, therefore 2

Back in grade 11 we learned the eq'n of a parabola was y=a(x-h)^2+b. Although this gets the job done back then, it does not provide us sufficient information when it comes to Conic Sections. y=a(x-h)^2+b can be expressed as the formula we use now, just to prove it is legitament.

y=a(x-h)^2+k

a(x-h)^2+k=y

a(x-h)^2=y-k

[(x-h)^2=(1/a)(y-k)]

That ended the first period. When we came back, we had a couple of questions on the board. These questions were incomplete squares with eq'ns that were un-usuable. We had to retrace our steps back a year to balance out the eq'n before we could find any information on them.

y^2+8x-6y+1=0 find... (work in red text to find the solutions to answers)

(y is the one ^2'd so it opens sideways) (if x was ^2'd it would open up or down)

Vertex;(1,3)

Focus;(-1,3) (vertex's x value -2) <-2=p (4p is negitive, therefore it opens left, parabola is around focus)

Eq'n Of Directrix;x=3, (vertex's x +2) <-2=p (4p is negitive, therefore it opens left, parabola opens away from directrix)

Eq'n of Axis of Sym;y=2 (axis of sym = vertex's y value if open sideways, x value if up or down)

Domain;(-oo, 1] (4p is negitive, therefore it opens left)

Range;(-oo, oo)

y^2+8x-6y+1=0

y^2-6y=-8x-1

y^2-6y+'9'=-8x-1+'9'

(y-3)^2=-8(x-1)

4p=-8, p=-2

The rest of the class consisted of a math dictionary insert, enjoy!

MATH DICTIONARY IS THE FOLLOWING:

Conic Sections

The word 'conic' means 'cone-like'. Four different types of cruves are generated by taking cross sections of a double napped cone. They are: i)Circles, ii)Ellipses, iii)Parabolas, iv)Hyperbolas

Locus: Set of points that follow a certain rules

Focus: A fixed point (or points) that determines a locus

Directrix: A fixed line that determines a Locus

Parabola: A locus of points that are equidistant from a fixed point (focus) and a fixed line (directrix)

The Anatomy of a Parabola

(x-h)^2=4p(y-k)

vertex(h-k)

focus(h,k+p)

eq'n of Directrix y=k-p

Eq'n of axis of sym: x=h

note: p

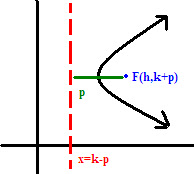
(y-k)^2=4p(x-h)

vertex (h,k)

focus (h,k+p)

eq'n of Directrix: x=k-p

eq'n of axis of sym: y=k

note: p

That ends it for today's scribe post~. It's really late now, i should wrap it up. Homework is Excercise the next =o, i believe it's called 'Parabola'. Serious of not, Mr.k said test was on friday, so learn hard this week! ScubaSteve out.